In the interest of reproducibility, and to showcase our new package `flotilla <http://github.com/yeolab/flotilla>`_, I’ve reproduced many figures from the landmark single-cell paper, Single-cell transcriptomics reveals bimodality in expression and splicing in immune cells by Shalek and Satija, et al. Nature (2013).
Before we begin, let’s import everything we need.
# Turn on inline plots with IPython
%matplotlib inline
# Import the flotilla package for biological data analysis
import flotilla
# Import "numerical python" library for number crunching
import numpy as np
# Import "panel data analysis" library for tabular data
import pandas as pd
# Import statistical data visualization package
# Note: As of November 6th, 2014, you will need the "master" version of
# seaborn on github (v0.5.dev), installed via
# "pip install git+ssh://git@github.com/mwaskom/seaborn.git
import seaborn as sns
Shalek and Satija, et al (2013)¶
In the 2013 paper, Single-cell transcriptomics reveals bimodality in expression and splicing in immune cells (Shalek and Satija, et al. Nature (2013)), Regev and colleagues performed single-cell sequencing 18 bone marrow-derived dendritic cells (BMDCs), in addition to 3 pooled samples.
Expression data¶
First, we will read in the expression data. These data were obtained using,
%%bash
wget ftp://ftp.ncbi.nlm.nih.gov/geo/series/GSE41nnn/GSE41265/suppl/GSE41265_allGenesTPM.txt.gz
--2015-06-09 22:42:47-- ftp://ftp.ncbi.nlm.nih.gov/geo/series/GSE41nnn/GSE41265/suppl/GSE41265_allGenesTPM.txt.gz
=> `GSE41265_allGenesTPM.txt.gz'
Resolving ftp.ncbi.nlm.nih.gov (ftp.ncbi.nlm.nih.gov)... 2607:f220:41e:250::13, 130.14.250.7
Connecting to ftp.ncbi.nlm.nih.gov (ftp.ncbi.nlm.nih.gov)|2607:f220:41e:250::13|:21... connected.
Logging in as anonymous ... Logged in!
==> SYST ... done. ==> PWD ... done.
==> TYPE I ... done. ==> CWD (1) /geo/series/GSE41nnn/GSE41265/suppl ... done.
==> SIZE GSE41265_allGenesTPM.txt.gz ... 1099290
==> EPSV ... done. ==> RETR GSE41265_allGenesTPM.txt.gz ... done.
Length: 1099290 (1.0M) (unauthoritative)
0K .......... .......... .......... .......... .......... 4% 969K 1s
50K .......... .......... .......... .......... .......... 9% 6.14M 1s
100K .......... .......... .......... .......... .......... 13% 6.28M 0s
150K .......... .......... .......... .......... .......... 18% 114M 0s
200K .......... .......... .......... .......... .......... 23% 6.45M 0s
250K .......... .......... .......... .......... .......... 27% 84.8M 0s
300K .......... .......... .......... .......... .......... 32% 6.99M 0s
350K .......... .......... .......... .......... .......... 37% 80.8M 0s
400K .......... .......... .......... .......... .......... 41% 112M 0s
450K .......... .......... .......... .......... .......... 46% 7.12M 0s
500K .......... .......... .......... .......... .......... 51% 102M 0s
550K .......... .......... .......... .......... .......... 55% 106M 0s
600K .......... .......... .......... .......... .......... 60% 91.3M 0s
650K .......... .......... .......... .......... .......... 65% 130M 0s
700K .......... .......... .......... .......... .......... 69% 7.88M 0s
750K .......... .......... .......... .......... .......... 74% 68.3M 0s
800K .......... .......... .......... .......... .......... 79% 96.2M 0s
850K .......... .......... .......... .......... .......... 83% 83.3M 0s
900K .......... .......... .......... .......... .......... 88% 84.6M 0s
950K .......... .......... .......... .......... .......... 93% 9.07M 0s
1000K .......... .......... .......... .......... .......... 97% 82.5M 0s
1050K .......... .......... ... 100% 190M=0.1s
2015-06-09 22:42:47 (9.77 MB/s) - `GSE41265_allGenesTPM.txt.gz' saved [1099290]
We will also compare to the supplementary table 2 data, obtained using
%%bash
wget http://www.nature.com/nature/journal/v498/n7453/extref/nature12172-s1.zip
unzip nature12172-s1.zip
Archive: nature12172-s1.zip
creating: nature12172-s1/
inflating: nature12172-s1/Supplementary_Table1.xls
inflating: nature12172-s1/Supplementary_Table2.xlsx
inflating: nature12172-s1/Supplementary_Table3.xls
inflating: nature12172-s1/Supplementary_Table4.xls
inflating: nature12172-s1/Supplementary_Table5.xls
inflating: nature12172-s1/Supplementary_Table6.xls
inflating: nature12172-s1/Supplementary_Table7.xlsx
--2015-06-09 22:42:47-- http://www.nature.com/nature/journal/v498/n7453/extref/nature12172-s1.zip
Resolving www.nature.com (www.nature.com)... 63.233.110.66, 63.233.110.80
Connecting to www.nature.com (www.nature.com)|63.233.110.66|:80... connected.
HTTP request sent, awaiting response... 200 OK
Length: 4634226 (4.4M) [application/zip]
Saving to: `nature12172-s1.zip'
0K .......... .......... .......... .......... .......... 1% 10.8M 0s
50K .......... .......... .......... .......... .......... 2% 22.3M 0s
100K .......... .......... .......... .......... .......... 3% 21.5M 0s
150K .......... .......... .......... .......... .......... 4% 21.9M 0s
200K .......... .......... .......... .......... .......... 5% 52.7M 0s
250K .......... .......... .......... .......... .......... 6% 7.57M 0s
300K .......... .......... .......... .......... .......... 7% 106M 0s
350K .......... .......... .......... .......... .......... 8% 25.1M 0s
400K .......... .......... .......... .......... .......... 9% 109M 0s
450K .......... .......... .......... .......... .......... 11% 26.4M 0s
500K .......... .......... .......... .......... .......... 12% 109M 0s
550K .......... .......... .......... .......... .......... 13% 80.5M 0s
600K .......... .......... .......... .......... .......... 14% 41.0M 0s
650K .......... .......... .......... .......... .......... 15% 71.4M 0s
700K .......... .......... .......... .......... .......... 16% 113M 0s
750K .......... .......... .......... .......... .......... 17% 95.8M 0s
800K .......... .......... .......... .......... .......... 18% 45.1M 0s
850K .......... .......... .......... .......... .......... 19% 122M 0s
900K .......... .......... .......... .......... .......... 20% 8.95M 0s
950K .......... .......... .......... .......... .......... 22% 67.4M 0s
1000K .......... .......... .......... .......... .......... 23% 108M 0s
1050K .......... .......... .......... .......... .......... 24% 98.4M 0s
1100K .......... .......... .......... .......... .......... 25% 115M 0s
1150K .......... .......... .......... .......... .......... 26% 53.9M 0s
1200K .......... .......... .......... .......... .......... 27% 57.1M 0s
1250K .......... .......... .......... .......... .......... 28% 96.1M 0s
1300K .......... .......... .......... .......... .......... 29% 196M 0s
1350K .......... .......... .......... .......... .......... 30% 138M 0s
1400K .......... .......... .......... .......... .......... 32% 133M 0s
1450K .......... .......... .......... .......... .......... 33% 121M 0s
1500K .......... .......... .......... .......... .......... 34% 93.9M 0s
1550K .......... .......... .......... .......... .......... 35% 5.29M 0s
1600K .......... .......... .......... .......... .......... 36% 128M 0s
1650K .......... .......... .......... .......... .......... 37% 97.5M 0s
1700K .......... .......... .......... .......... .......... 38% 78.8M 0s
1750K .......... .......... .......... .......... .......... 39% 117M 0s
1800K .......... .......... .......... .......... .......... 40% 95.6M 0s
1850K .......... .......... .......... .......... .......... 41% 120M 0s
1900K .......... .......... .......... .......... .......... 43% 85.1M 0s
1950K .......... .......... .......... .......... .......... 44% 80.9M 0s
2000K .......... .......... .......... .......... .......... 45% 126M 0s
2050K .......... .......... .......... .......... .......... 46% 8.80M 0s
2100K .......... .......... .......... .......... .......... 47% 129M 0s
2150K .......... .......... .......... .......... .......... 48% 88.2M 0s
2200K .......... .......... .......... .......... .......... 49% 39.6M 0s
2250K .......... .......... .......... .......... .......... 50% 80.0M 0s
2300K .......... .......... .......... .......... .......... 51% 116M 0s
2350K .......... .......... .......... .......... .......... 53% 88.2M 0s
2400K .......... .......... .......... .......... .......... 54% 88.7M 0s
2450K .......... .......... .......... .......... .......... 55% 5.20M 0s
2500K .......... .......... .......... .......... .......... 56% 84.0M 0s
2550K .......... .......... .......... .......... .......... 57% 99.7M 0s
2600K .......... .......... .......... .......... .......... 58% 62.1M 0s
2650K .......... .......... .......... .......... .......... 59% 75.6M 0s
2700K .......... .......... .......... .......... .......... 60% 99.2M 0s
2750K .......... .......... .......... .......... .......... 61% 81.9M 0s
2800K .......... .......... .......... .......... .......... 62% 118M 0s
2850K .......... .......... .......... .......... .......... 64% 89.6M 0s
2900K .......... .......... .......... .......... .......... 65% 117M 0s
2950K .......... .......... .......... .......... .......... 66% 91.5M 0s
3000K .......... .......... .......... .......... .......... 67% 123M 0s
3050K .......... .......... .......... .......... .......... 68% 84.1M 0s
3100K .......... .......... .......... .......... .......... 69% 118M 0s
3150K .......... .......... .......... .......... .......... 70% 128M 0s
3200K .......... .......... .......... .......... .......... 71% 96.6M 0s
3250K .......... .......... .......... .......... .......... 72% 37.8M 0s
3300K .......... .......... .......... .......... .......... 74% 64.9M 0s
3350K .......... .......... .......... .......... .......... 75% 121M 0s
3400K .......... .......... .......... .......... .......... 76% 3.82M 0s
3450K .......... .......... .......... .......... .......... 77% 93.9M 0s
3500K .......... .......... .......... .......... .......... 78% 129M 0s
3550K .......... .......... .......... .......... .......... 79% 79.8M 0s
3600K .......... .......... .......... .......... .......... 80% 113M 0s
3650K .......... .......... .......... .......... .......... 81% 104M 0s
3700K .......... .......... .......... .......... .......... 82% 82.3M 0s
3750K .......... .......... .......... .......... .......... 83% 116M 0s
3800K .......... .......... .......... .......... .......... 85% 122M 0s
3850K .......... .......... .......... .......... .......... 86% 92.9M 0s
3900K .......... .......... .......... .......... .......... 87% 110M 0s
3950K .......... .......... .......... .......... .......... 88% 93.3M 0s
4000K .......... .......... .......... .......... .......... 89% 88.7M 0s
4050K .......... .......... .......... .......... .......... 90% 23.4M 0s
4100K .......... .......... .......... .......... .......... 91% 89.4M 0s
4150K .......... .......... .......... .......... .......... 92% 8.52M 0s
4200K .......... .......... .......... .......... .......... 93% 122M 0s
4250K .......... .......... .......... .......... .......... 95% 126M 0s
4300K .......... .......... .......... .......... .......... 96% 11.9M 0s
4350K .......... .......... .......... .......... .......... 97% 79.5M 0s
4400K .......... .......... .......... .......... .......... 98% 115M 0s
4450K .......... .......... .......... .......... .......... 99% 88.9M 0s
4500K .......... .......... ..... 100% 112M=0.1s
2015-06-09 22:42:47 (37.7 MB/s) - `nature12172-s1.zip' saved [4634226/4634226]
expression = pd.read_table("GSE41265_allGenesTPM.txt.gz", compression="gzip", index_col=0)
expression.head()
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | ... | S12 | S13 | S14 | S15 | S16 | S17 | S18 | P1 | P2 | P3 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GENE | |||||||||||||||||||||
| XKR4 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.019906 | 0.000000 |
| AB338584 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| B3GAT2 | 0.000000 | 0.000000 | 0.023441 | 0.000000 | 0.000000 | 0.029378 | 0.000000 | 0.055452 | 0.000000 | 0.029448 | ... | 0.000000 | 0.000000 | 0.031654 | 0.000000 | 0.000000 | 0.000000 | 42.150208 | 0.680327 | 0.022996 | 0.110236 |
| NPL | 72.008590 | 0.000000 | 128.062012 | 0.095082 | 0.000000 | 0.000000 | 112.310234 | 104.329122 | 0.119230 | 0.000000 | ... | 0.000000 | 0.116802 | 0.104200 | 0.106188 | 0.229197 | 0.110582 | 0.000000 | 7.109356 | 6.727028 | 14.525447 |
| T2 | 0.109249 | 0.172009 | 0.000000 | 0.000000 | 0.182703 | 0.076012 | 0.078698 | 0.000000 | 0.093698 | 0.076583 | ... | 0.693459 | 0.010137 | 0.081936 | 0.000000 | 0.000000 | 0.086879 | 0.068174 | 0.062063 | 0.000000 | 0.050605 |
5 rows × 21 columns
These data are in the “transcripts per million,” aka TPM unit. See this blog post if that sounds weird to you.
These data are formatted with samples on the columns, and genes on the rows. But we want the opposite, with samples on the rows and genes on the columns. This follows `scikit-learn <http://scikit-learn.org/stable/tutorial/basic/tutorial.html#loading-an-example-dataset>`_’s standard of data matrices with size (n_samples, n_features) as each gene is a feature. So we will simply transpose this.
expression = expression.T
expression.head()
| GENE | XKR4 | AB338584 | B3GAT2 | NPL | T2 | T | PDE10A | 1700010I14RIK | 6530411M01RIK | PABPC6 | ... | AK085062 | DHX9 | RNASET2B | FGFR1OP | CCR6 | BRP44L | AK014435 | AK015714 | SFT2D1 | PRR18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S1 | 0 | 0 | 0.000000 | 72.008590 | 0.109249 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0.774638 | 23.520936 | 0.000000 | 0 | 460.316773 | 0 | 0.000000 | 39.442566 | 0 |
| S2 | 0 | 0 | 0.000000 | 0.000000 | 0.172009 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0.367391 | 1.887873 | 0.000000 | 0 | 823.890290 | 0 | 0.000000 | 4.967412 | 0 |
| S3 | 0 | 0 | 0.023441 | 128.062012 | 0.000000 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0.249858 | 0.313510 | 0.166772 | 0 | 1002.354241 | 0 | 0.000000 | 0.000000 | 0 |
| S4 | 0 | 0 | 0.000000 | 0.095082 | 0.000000 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0.354157 | 0.000000 | 0.887003 | 0 | 1230.766795 | 0 | 0.000000 | 0.131215 | 0 |
| S5 | 0 | 0 | 0.000000 | 0.000000 | 0.182703 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0.039263 | 0.000000 | 131.077131 | 0 | 1614.749122 | 0 | 0.242179 | 95.485743 | 0 |
5 rows × 27723 columns
The authors filtered the expression data based on having at least 3 single cells express genes with at TPM (transcripts per million, ) > 1. We can express this in using the `pandas <http://pandas.pydata.org>`_ DataFrames easily.
First, from reading the paper and looking at the data, I know there are 18 single cells, and there are 18 samples that start with the letter “S.” So I will extract the single samples from the index (row names) using a lambda, a tiny function which in this case, tells me whether or not that sample id begins with the letter “S”.
singles_ids = expression.index[expression.index.map(lambda x: x.startswith('S'))]
print('number of single cells:', len(singles_ids))
singles = expression.ix[singles_ids]
expression_filtered = expression.ix[:, singles[singles > 1].count() >= 3]
expression_filtered = np.log(expression_filtered + 1)
expression_filtered.shape
('number of single cells:', 18)
(21, 6312)
Hmm, that’s strange. The paper states that they had 6313 genes after filtering, but I get 6312. Even using “singles >= 1” doesn’t help.
(I also tried this with the expression table provided in the supplementary data as “SupplementaryTable2.xlsx,” and got the same results.)
Now that we’ve taken care of importing and filtering the expression data, let’s do the feature data of the expression data.
Expression feature data¶
This is similar to the fData from BioconductoR, where there’s some additional data on your features that you want to look at. They uploaded information about the features in their OTHER expression matrix, uploaded as a supplementary file, Supplementary_Table2.xlsx.
Notice that this is a csv and not an xlsx. This is because Excel mangled the gene IDS that started with 201* and assumed they were dates :(
The workaround I did was to add another column to the sheet with the formula ="'" & A1, press Command-Shift-End to select the end of the rows, and then do Ctrl-D to “fill down” to the bottom (thanks to this stackoverflow post for teaching me how to Excel). Then, I saved the file as a csv for maximum portability and compatibility.
So sorry, this requires some non-programming editing! But I’ve posted the csv to our github repo with all the data, and we’ll access it from there.
expression2 = pd.read_csv('https://raw.githubusercontent.com/YeoLab/shalek2013/master/Supplementary_Table2.csv',
# Need to specify the index column as both the first and the last columns,
# Because the last column is the "Gene Category"
index_col=[0, -1], parse_dates=False, infer_datetime_format=False)
# This was also in features x samples format, so we need to transpose
expression2 = expression2.T
expression2.head()
| 'GENE | '0610007L01RIK | '0610007P14RIK | '0610007P22RIK | '0610008F07RIK | '0610009B22RIK | '0610009D07RIK | '0610009O20RIK | '0610010B08RIK | '0610010F05RIK | '0610010K06RIK | ... | 'ZWILCH | 'ZWINT | 'ZXDA | 'ZXDB | 'ZXDC | 'ZYG11A | 'ZYG11B | 'ZYX | 'ZZEF1 | 'ZZZ3 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Gene Category | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| S1 | 27.181570 | 0.166794 | 0 | 0 | 0.000000 | 178.852732 | 0 | 0.962417 | 0.000000 | 143.359550 | ... | 0.000000 | 302.361227 | 0.000000 | 0 | 0 | 0 | 0.027717 | 297.918756 | 37.685501 | 0.000000 |
| S2 | 37.682691 | 0.263962 | 0 | 0 | 0.207921 | 0.141099 | 0 | 0.000000 | 0.000000 | 0.255617 | ... | 0.000000 | 96.033724 | 0.020459 | 0 | 0 | 0 | 0.042430 | 0.242888 | 0.000000 | 0.000000 |
| S3 | 0.056916 | 78.622459 | 0 | 0 | 0.145680 | 0.396363 | 0 | 0.000000 | 0.024692 | 72.775846 | ... | 0.000000 | 427.915555 | 0.000000 | 0 | 0 | 0 | 0.040407 | 6.753530 | 0.132011 | 0.017615 |
| S4 | 55.649250 | 0.228866 | 0 | 0 | 0.000000 | 88.798158 | 0 | 0.000000 | 0.000000 | 93.825442 | ... | 0.000000 | 9.788557 | 0.017787 | 0 | 0 | 0 | 0.013452 | 0.274689 | 9.724890 | 0.000000 |
| S5 | 0.000000 | 0.093117 | 0 | 0 | 131.326008 | 155.936361 | 0 | 0.000000 | 0.000000 | 0.031029 | ... | 0.204522 | 26.575760 | 0.000000 | 0 | 0 | 0 | 1.101589 | 59.256094 | 44.430726 | 0.000000 |
5 rows × 27723 columns
Now we need to strip the single-quote I added to all the gene names:
new_index, indexer = expression2.columns.reindex(map(lambda x: (x[0].lstrip("'"), x[1]), expression2.columns.values))
expression2.columns = new_index
expression2.head()
| 'GENE | 0610007L01RIK | 0610007P14RIK | 0610007P22RIK | 0610008F07RIK | 0610009B22RIK | 0610009D07RIK | 0610009O20RIK | 0610010B08RIK | 0610010F05RIK | 0610010K06RIK | ... | ZWILCH | ZWINT | ZXDA | ZXDB | ZXDC | ZYG11A | ZYG11B | ZYX | ZZEF1 | ZZZ3 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Gene Category | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| S1 | 27.181570 | 0.166794 | 0 | 0 | 0.000000 | 178.852732 | 0 | 0.962417 | 0.000000 | 143.359550 | ... | 0.000000 | 302.361227 | 0.000000 | 0 | 0 | 0 | 0.027717 | 297.918756 | 37.685501 | 0.000000 |
| S2 | 37.682691 | 0.263962 | 0 | 0 | 0.207921 | 0.141099 | 0 | 0.000000 | 0.000000 | 0.255617 | ... | 0.000000 | 96.033724 | 0.020459 | 0 | 0 | 0 | 0.042430 | 0.242888 | 0.000000 | 0.000000 |
| S3 | 0.056916 | 78.622459 | 0 | 0 | 0.145680 | 0.396363 | 0 | 0.000000 | 0.024692 | 72.775846 | ... | 0.000000 | 427.915555 | 0.000000 | 0 | 0 | 0 | 0.040407 | 6.753530 | 0.132011 | 0.017615 |
| S4 | 55.649250 | 0.228866 | 0 | 0 | 0.000000 | 88.798158 | 0 | 0.000000 | 0.000000 | 93.825442 | ... | 0.000000 | 9.788557 | 0.017787 | 0 | 0 | 0 | 0.013452 | 0.274689 | 9.724890 | 0.000000 |
| S5 | 0.000000 | 0.093117 | 0 | 0 | 131.326008 | 155.936361 | 0 | 0.000000 | 0.000000 | 0.031029 | ... | 0.204522 | 26.575760 | 0.000000 | 0 | 0 | 0 | 1.101589 | 59.256094 | 44.430726 | 0.000000 |
5 rows × 27723 columns
We want to create a pandas.DataFrame from the “Gene Category” row for our expression_feature_data, which we will do via:
gene_ids, gene_category = zip(*expression2.columns.values)
gene_categories = pd.Series(gene_category, index=gene_ids, name='gene_category')
gene_categories
0610007L01RIK NaN
0610007P14RIK NaN
0610007P22RIK NaN
0610008F07RIK NaN
0610009B22RIK NaN
0610009D07RIK NaN
0610009O20RIK NaN
0610010B08RIK NaN
0610010F05RIK NaN
0610010K06RIK NaN
0610010K14RIK NaN
0610010O12RIK NaN
0610011F06RIK NaN
0610011L14RIK NaN
0610012G03RIK NaN
0610012H03RIK NaN
0610030E20RIK NaN
0610031J06RIK NaN
0610037L13RIK NaN
0610037P05RIK NaN
0610038B21RIK NaN
0610039K10RIK NaN
0610040B10RIK NaN
0610040J01RIK NaN
0910001L09RIK NaN
100043387 NaN
1100001G20RIK NaN
1110001A16RIK NaN
1110001J03RIK NaN
1110002B05RIK NaN
...
ZSCAN20 NaN
ZSCAN21 NaN
ZSCAN22 NaN
ZSCAN29 NaN
ZSCAN30 NaN
ZSCAN4B NaN
ZSCAN4C NaN
ZSCAN4D NaN
ZSCAN4E NaN
ZSCAN4F NaN
ZSCAN5B NaN
ZSWIM1 NaN
ZSWIM2 NaN
ZSWIM3 NaN
ZSWIM4 NaN
ZSWIM5 NaN
ZSWIM6 NaN
ZSWIM7 NaN
ZUFSP LPS Response
ZW10 NaN
ZWILCH NaN
ZWINT NaN
ZXDA NaN
ZXDB NaN
ZXDC NaN
ZYG11A NaN
ZYG11B NaN
ZYX NaN
ZZEF1 NaN
ZZZ3 NaN
Name: gene_category, dtype: object
expression_feature_data = pd.DataFrame(gene_categories)
expression_feature_data.head()
| gene_category | |
|---|---|
| 0610007L01RIK | NaN |
| 0610007P14RIK | NaN |
| 0610007P22RIK | NaN |
| 0610008F07RIK | NaN |
| 0610009B22RIK | NaN |
Splicing Data¶
We obtain the splicing data from this study from the supplementary information, specifically the Supplementary_Table4.xls
splicing = pd.read_excel('nature12172-s1/Supplementary_Table4.xls', 'splicingTable.txt', index_col=(0,1))
splicing.head()
---------------------------------------------------------------------------
ImportError Traceback (most recent call last)
<ipython-input-11-6956dd3a6ad6> in <module>()
----> 1 splicing = pd.read_excel('nature12172-s1/Supplementary_Table4.xls', 'splicingTable.txt', index_col=(0,1))
2 splicing.head()
/home/travis/miniconda/envs/testenv/lib/python2.7/site-packages/pandas/io/excel.pyc in read_excel(io, sheetname, **kwds)
149 engine = kwds.pop('engine', None)
150
--> 151 return ExcelFile(io, engine=engine).parse(sheetname=sheetname, **kwds)
152
153
/home/travis/miniconda/envs/testenv/lib/python2.7/site-packages/pandas/io/excel.pyc in __init__(self, io, **kwds)
167 def __init__(self, io, **kwds):
168
--> 169 import xlrd # throw an ImportError if we need to
170
171 ver = tuple(map(int, xlrd.__VERSION__.split(".")[:2]))
ImportError: No module named xlrd
splicing = splicing.T
splicing
| Event name | chr10:126534988:126535177:-@chr10:126533971:126534135:-@chr10:126533686:126533798:- | chr10:14403870:14403945:-@chr10:14395740:14395848:-@chr10:14387738:14387914:- | chr10:20051892:20052067:+@chr10:20052202:20052363:+@chr10:20053198:20053697:+ | chr10:20052864:20053378:+@chr10:20054305:20054451:+@chr10:20059515:20059727:+ | chr10:58814831:58815007:+@chr10:58817088:58817158:+@chr10:58818098:58818168:+@chr10:58824609:58824708:+ | chr10:79173370:79173665:+@chr10:79174001:79174029:+@chr10:79174239:79174726:+ | chr10:79322526:79322700:+@chr10:79322862:79322939:+@chr10:79323569:79323862:+ | chr10:87376364:87376545:+@chr10:87378043:87378094:+@chr10:87393420:87399792:+ | chr10:92747514:92747722:-@chr10:92727625:92728425:-@chr10:92717434:92717556:- | chr11:101438508:101438565:+@chr11:101439246:101439351:+@chr11:101441899:101443267:+ | ... | chr8:126022488:126022598:+@chr8:126023892:126024007:+@chr8:126025133:126025333:+ | chr14:51455667:51455879:-@chr14:51453589:51453752:-@chr14:51453129:51453242:- | chr17:29497858:29498102:+@chr17:29500656:29500887:+@chr17:29501856:29502226:+ | chr2:94198908:94199094:-@chr2:94182784:94182954:-@chr2:94172950:94173209:- | chr9:21314438:21314697:-@chr9:21313375:21313558:-@chr9:21311823:21312835:- | chr9:21314438:21314697:-@chr9:21313375:21313795:-@chr9:21311823:21312835:- | chr10:79545360:79545471:-@chr10:79542698:79544127:-@chr10:79533365:79535263:- | chr17:5975579:5975881:+@chr17:5985972:5986242:+@chr17:5990136:5990361:+ | chr2:29997782:29997941:+@chr2:30002172:30002382:+@chr2:30002882:30003045:+ | chr7:119221306:119221473:+@chr7:119223686:119223745:+@chr7:119225944:119226075:+ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| gene | Os9 | Vta1 | Bclaf1 | Bclaf1 | P4ha1 | Bsg | Ptbp1 | Igf1 | Elk3 | Nbr1 | ... | Afg3l1 | Tep1 | Fgd2 | Ttc17 | Tmed1 | Tmed1 | Sbno2 | Synj2 | Tbc1d13 | Usp47 |
| S1 | 0.84 | 0.95 | NaN | 0.02 | 0.42 | NaN | 0.57 | 0.31 | 0.93 | 0.57 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| S2 | NaN | NaN | 0.04 | 0.98 | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| S3 | NaN | NaN | 0.02 | 0.55 | NaN | NaN | NaN | 0.20 | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| S4 | NaN | 0.84 | NaN | NaN | NaN | NaN | NaN | 0.95 | NaN | 0.04 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| S5 | NaN | 0.95 | NaN | NaN | 0.94 | NaN | NaN | 0.73 | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| S6 | 0.01 | 0.91 | 0.14 | NaN | NaN | NaN | NaN | 0.61 | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| S7 | NaN | 0.87 | NaN | NaN | NaN | 0.62 | NaN | 0.85 | 0.73 | 0.55 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| S8 | NaN | 0.86 | 0.02 | 0.98 | 0.03 | NaN | NaN | 0.89 | 0.82 | 0.83 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| S9 | NaN | NaN | NaN | NaN | 0.97 | NaN | 0.97 | NaN | 0.90 | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| S10 | NaN | NaN | NaN | NaN | NaN | NaN | 0.06 | 0.98 | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| S11 | 0.03 | 0.93 | NaN | NaN | NaN | NaN | NaN | NaN | 0.97 | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| S13 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| S14 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.88 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| S15 | 0.02 | 0.96 | 0.01 | 0.06 | NaN | NaN | NaN | 0.44 | NaN | NaN | ... | 0.91 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| S16 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | 0.27 | 0.99 | 0.99 | 0.98 | 0.98 | NaN | NaN | NaN | NaN |
| S17 | 0.01 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | 0.96 | NaN | NaN | NaN | 0.99 | 0.98 | 0.67 | 0.07 |
| S18 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 10,000 cell Rep1 (P1) | 0.27 | 0.83 | 0.40 | 0.62 | 0.43 | 0.78 | NaN | 0.60 | 0.76 | 0.52 | ... | 0.92 | NaN | 0.81 | 0.77 | NaN | NaN | 0.84 | 0.50 | 0.56 | NaN |
| 10,000 cell Rep2 (P2) | 0.37 | 0.85 | 0.49 | 0.63 | 0.36 | 0.72 | 0.47 | 0.60 | 0.73 | 0.68 | ... | 0.67 | 0.15 | 0.52 | 0.67 | 0.63 | 0.73 | 0.82 | 0.90 | 0.71 | 0.55 |
| 10,000 cell Rep3 (P3) | 0.31 | 0.64 | 0.59 | 0.70 | 0.52 | 0.79 | NaN | 0.65 | 0.42 | 0.64 | ... | 0.58 | 0.79 | 0.74 | 0.85 | 0.73 | 0.39 | 0.56 | NaN | 0.64 | NaN |
20 rows × 352 columns
The three pooled samples aren’t named consistently with the expression data, so we have to fix that.
splicing.index[splicing.index.map(lambda x: 'P' in x)]
Index([u'10,000 cell Rep1 (P1)', u'10,000 cell Rep2 (P2)', u'10,000 cell Rep3 (P3)'], dtype='object')
Since the pooled sample IDs are inconsistent with the expression data, we have to change them. We can get the “P” and the number after that using regular expressions, called re in the Python standard library, e.g.:
import re
re.search(r'P\d', '10,000 cell Rep1 (P1)').group()
'P1'
def long_pooled_name_to_short(x):
if 'P' not in x:
return x
else:
return re.search(r'P\d', x).group()
splicing.index.map(long_pooled_name_to_short)
array([u'S1', u'S2', u'S3', u'S4', u'S5', u'S6', u'S7', u'S8', u'S9',
u'S10', u'S11', u'S13', u'S14', u'S15', u'S16', u'S17', u'S18',
u'P1', u'P2', u'P3'], dtype=object)
And now we assign this new index as our index to the splicing dataframe
splicing.index = splicing.index.map(long_pooled_name_to_short)
splicing.head()
| Event name | chr10:126534988:126535177:-@chr10:126533971:126534135:-@chr10:126533686:126533798:- | chr10:14403870:14403945:-@chr10:14395740:14395848:-@chr10:14387738:14387914:- | chr10:20051892:20052067:+@chr10:20052202:20052363:+@chr10:20053198:20053697:+ | chr10:20052864:20053378:+@chr10:20054305:20054451:+@chr10:20059515:20059727:+ | chr10:58814831:58815007:+@chr10:58817088:58817158:+@chr10:58818098:58818168:+@chr10:58824609:58824708:+ | chr10:79173370:79173665:+@chr10:79174001:79174029:+@chr10:79174239:79174726:+ | chr10:79322526:79322700:+@chr10:79322862:79322939:+@chr10:79323569:79323862:+ | chr10:87376364:87376545:+@chr10:87378043:87378094:+@chr10:87393420:87399792:+ | chr10:92747514:92747722:-@chr10:92727625:92728425:-@chr10:92717434:92717556:- | chr11:101438508:101438565:+@chr11:101439246:101439351:+@chr11:101441899:101443267:+ | ... | chr8:126022488:126022598:+@chr8:126023892:126024007:+@chr8:126025133:126025333:+ | chr14:51455667:51455879:-@chr14:51453589:51453752:-@chr14:51453129:51453242:- | chr17:29497858:29498102:+@chr17:29500656:29500887:+@chr17:29501856:29502226:+ | chr2:94198908:94199094:-@chr2:94182784:94182954:-@chr2:94172950:94173209:- | chr9:21314438:21314697:-@chr9:21313375:21313558:-@chr9:21311823:21312835:- | chr9:21314438:21314697:-@chr9:21313375:21313795:-@chr9:21311823:21312835:- | chr10:79545360:79545471:-@chr10:79542698:79544127:-@chr10:79533365:79535263:- | chr17:5975579:5975881:+@chr17:5985972:5986242:+@chr17:5990136:5990361:+ | chr2:29997782:29997941:+@chr2:30002172:30002382:+@chr2:30002882:30003045:+ | chr7:119221306:119221473:+@chr7:119223686:119223745:+@chr7:119225944:119226075:+ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| gene | Os9 | Vta1 | Bclaf1 | Bclaf1 | P4ha1 | Bsg | Ptbp1 | Igf1 | Elk3 | Nbr1 | ... | Afg3l1 | Tep1 | Fgd2 | Ttc17 | Tmed1 | Tmed1 | Sbno2 | Synj2 | Tbc1d13 | Usp47 |
| S1 | 0.84 | 0.95 | NaN | 0.02 | 0.42 | NaN | 0.57 | 0.31 | 0.93 | 0.57 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| S2 | NaN | NaN | 0.04 | 0.98 | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| S3 | NaN | NaN | 0.02 | 0.55 | NaN | NaN | NaN | 0.20 | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| S4 | NaN | 0.84 | NaN | NaN | NaN | NaN | NaN | 0.95 | NaN | 0.04 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| S5 | NaN | 0.95 | NaN | NaN | 0.94 | NaN | NaN | 0.73 | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
5 rows × 352 columns
Remove Multi-index columns¶
Currently, flotilla only supports non-multi-index Dataframes. This means that we need to change the columns of splicing to just the unique event name. We’ll save this data as splicing_feature_data, which will rename the crazy feature id to the reasonable gene name.
Splicing Feature Data¶
First, let’s extract the event names and gene names from splicing.
event_names, gene_names = zip(*splicing.columns.tolist())
event_names[:10]
(u'chr10:126534988:126535177:-@chr10:126533971:126534135:-@chr10:126533686:126533798:-',
u'chr10:14403870:14403945:-@chr10:14395740:14395848:-@chr10:14387738:14387914:-',
u'chr10:20051892:20052067:+@chr10:20052202:20052363:+@chr10:20053198:20053697:+',
u'chr10:20052864:20053378:+@chr10:20054305:20054451:+@chr10:20059515:20059727:+',
u'chr10:58814831:58815007:+@chr10:58817088:58817158:+@chr10:58818098:58818168:+@chr10:58824609:58824708:+',
u'chr10:79173370:79173665:+@chr10:79174001:79174029:+@chr10:79174239:79174726:+',
u'chr10:79322526:79322700:+@chr10:79322862:79322939:+@chr10:79323569:79323862:+',
u'chr10:87376364:87376545:+@chr10:87378043:87378094:+@chr10:87393420:87399792:+',
u'chr10:92747514:92747722:-@chr10:92727625:92728425:-@chr10:92717434:92717556:-',
u'chr11:101438508:101438565:+@chr11:101439246:101439351:+@chr11:101441899:101443267:+')
gene_names[:10]
(u'Os9',
u'Vta1',
u'Bclaf1',
u'Bclaf1',
u'P4ha1',
u'Bsg',
u'Ptbp1',
u'Igf1',
u'Elk3',
u'Nbr1')
Now we can rename the columns of splicing easily
splicing.columns = event_names
splicing.head()
| chr10:126534988:126535177:-@chr10:126533971:126534135:-@chr10:126533686:126533798:- | chr10:14403870:14403945:-@chr10:14395740:14395848:-@chr10:14387738:14387914:- | chr10:20051892:20052067:+@chr10:20052202:20052363:+@chr10:20053198:20053697:+ | chr10:20052864:20053378:+@chr10:20054305:20054451:+@chr10:20059515:20059727:+ | chr10:58814831:58815007:+@chr10:58817088:58817158:+@chr10:58818098:58818168:+@chr10:58824609:58824708:+ | chr10:79173370:79173665:+@chr10:79174001:79174029:+@chr10:79174239:79174726:+ | chr10:79322526:79322700:+@chr10:79322862:79322939:+@chr10:79323569:79323862:+ | chr10:87376364:87376545:+@chr10:87378043:87378094:+@chr10:87393420:87399792:+ | chr10:92747514:92747722:-@chr10:92727625:92728425:-@chr10:92717434:92717556:- | chr11:101438508:101438565:+@chr11:101439246:101439351:+@chr11:101441899:101443267:+ | ... | chr8:126022488:126022598:+@chr8:126023892:126024007:+@chr8:126025133:126025333:+ | chr14:51455667:51455879:-@chr14:51453589:51453752:-@chr14:51453129:51453242:- | chr17:29497858:29498102:+@chr17:29500656:29500887:+@chr17:29501856:29502226:+ | chr2:94198908:94199094:-@chr2:94182784:94182954:-@chr2:94172950:94173209:- | chr9:21314438:21314697:-@chr9:21313375:21313558:-@chr9:21311823:21312835:- | chr9:21314438:21314697:-@chr9:21313375:21313795:-@chr9:21311823:21312835:- | chr10:79545360:79545471:-@chr10:79542698:79544127:-@chr10:79533365:79535263:- | chr17:5975579:5975881:+@chr17:5985972:5986242:+@chr17:5990136:5990361:+ | chr2:29997782:29997941:+@chr2:30002172:30002382:+@chr2:30002882:30003045:+ | chr7:119221306:119221473:+@chr7:119223686:119223745:+@chr7:119225944:119226075:+ | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S1 | 0.84 | 0.95 | NaN | 0.02 | 0.42 | NaN | 0.57 | 0.31 | 0.93 | 0.57 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| S2 | NaN | NaN | 0.04 | 0.98 | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| S3 | NaN | NaN | 0.02 | 0.55 | NaN | NaN | NaN | 0.20 | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| S4 | NaN | 0.84 | NaN | NaN | NaN | NaN | NaN | 0.95 | NaN | 0.04 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| S5 | NaN | 0.95 | NaN | NaN | 0.94 | NaN | NaN | 0.73 | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
5 rows × 352 columns
Now let’s create splicing_feature_data to map these event names to the gene names, and to the gene_category from before.
splicing_feature_data = pd.DataFrame(index=event_names)
splicing_feature_data['gene_name'] = gene_names
splicing_feature_data.head()
| gene_name | |
|---|---|
| chr10:126534988:126535177:-@chr10:126533971:126534135:-@chr10:126533686:126533798:- | Os9 |
| chr10:14403870:14403945:-@chr10:14395740:14395848:-@chr10:14387738:14387914:- | Vta1 |
| chr10:20051892:20052067:+@chr10:20052202:20052363:+@chr10:20053198:20053697:+ | Bclaf1 |
| chr10:20052864:20053378:+@chr10:20054305:20054451:+@chr10:20059515:20059727:+ | Bclaf1 |
| chr10:58814831:58815007:+@chr10:58817088:58817158:+@chr10:58818098:58818168:+@chr10:58824609:58824708:+ | P4ha1 |
One thing we need to keep in mind is that the gene names in the expression data were uppercase. We can convert our gene names to uppercase with,`
splicing_feature_data['gene_name'] = splicing_feature_data['gene_name'].str.upper()
splicing_feature_data.head()
| gene_name | |
|---|---|
| chr10:126534988:126535177:-@chr10:126533971:126534135:-@chr10:126533686:126533798:- | OS9 |
| chr10:14403870:14403945:-@chr10:14395740:14395848:-@chr10:14387738:14387914:- | VTA1 |
| chr10:20051892:20052067:+@chr10:20052202:20052363:+@chr10:20053198:20053697:+ | BCLAF1 |
| chr10:20052864:20053378:+@chr10:20054305:20054451:+@chr10:20059515:20059727:+ | BCLAF1 |
| chr10:58814831:58815007:+@chr10:58817088:58817158:+@chr10:58818098:58818168:+@chr10:58824609:58824708:+ | P4HA1 |
Now let’s get the gene_category of these genes by doing a join on the splicing data and the expression data.
splicing_feature_data = splicing_feature_data.join(expression_feature_data, on='gene_name')
splicing_feature_data.head()
| gene_name | gene_category | |
|---|---|---|
| chr10:126534988:126535177:-@chr10:126533971:126534135:-@chr10:126533686:126533798:- | OS9 | NaN |
| chr10:14403870:14403945:-@chr10:14395740:14395848:-@chr10:14387738:14387914:- | VTA1 | NaN |
| chr10:20051892:20052067:+@chr10:20052202:20052363:+@chr10:20053198:20053697:+ | BCLAF1 | NaN |
| chr10:20052864:20053378:+@chr10:20054305:20054451:+@chr10:20059515:20059727:+ | BCLAF1 | NaN |
| chr10:58814831:58815007:+@chr10:58817088:58817158:+@chr10:58818098:58818168:+@chr10:58824609:58824708:+ | P4HA1 | LPS Response |
Now we have the gene_category encoded in the splicing data as well!
Metadata¶
Now let’s get into creating a metadata dataframe. We’ll use the index from the expression_filtered data to create the minimum required column, 'phenotype', which has the name of the phenotype of that cell. And we’ll also add the column 'pooled' to indicate whether this sample is pooled or not.
metadata = pd.DataFrame(index=expression_filtered.index)
metadata['phenotype'] = 'BDMC'
metadata['pooled'] = metadata.index.map(lambda x: x.startswith('P'))
metadata
| phenotype | pooled | |
|---|---|---|
| S1 | BDMC | False |
| S2 | BDMC | False |
| S3 | BDMC | False |
| S4 | BDMC | False |
| S5 | BDMC | False |
| S6 | BDMC | False |
| S7 | BDMC | False |
| S8 | BDMC | False |
| S9 | BDMC | False |
| S10 | BDMC | False |
| S11 | BDMC | False |
| S12 | BDMC | False |
| S13 | BDMC | False |
| S14 | BDMC | False |
| S15 | BDMC | False |
| S16 | BDMC | False |
| S17 | BDMC | False |
| S18 | BDMC | False |
| P1 | BDMC | True |
| P2 | BDMC | True |
| P3 | BDMC | True |
Mapping stats data¶
mapping_stats = pd.read_excel('nature12172-s1/Supplementary_Table1.xls', sheetname='SuppTable1 2.txt')
mapping_stats
| Sample | PF_READS | PCT_MAPPED_GENOME | PCT_RIBOSOMAL_BASES | MEDIAN_CV_COVERAGE | MEDIAN_5PRIME_BIAS | MEDIAN_3PRIME_BIAS | MEDIAN_5PRIME_TO_3PRIME_BIAS | |
|---|---|---|---|---|---|---|---|---|
| 0 | S1 | 21326048 | 0.706590 | 0.006820 | 0.509939 | 0.092679 | 0.477321 | 0.247741 |
| 1 | S2 | 27434011 | 0.745385 | 0.004111 | 0.565732 | 0.056583 | 0.321053 | 0.244062 |
| 2 | S3 | 31142391 | 0.722087 | 0.006428 | 0.540341 | 0.079551 | 0.382286 | 0.267367 |
| 3 | S4 | 26231852 | 0.737854 | 0.004959 | 0.530978 | 0.067041 | 0.351670 | 0.279782 |
| 4 | S5 | 29977214 | 0.746466 | 0.006121 | 0.525598 | 0.066543 | 0.353995 | 0.274252 |
| 5 | S6 | 24148387 | 0.730079 | 0.008794 | 0.529650 | 0.072095 | 0.413696 | 0.225929 |
| 6 | S7 | 24078116 | 0.730638 | 0.007945 | 0.540913 | 0.051991 | 0.358597 | 0.201984 |
| 7 | S8 | 25032126 | 0.739989 | 0.004133 | 0.512725 | 0.058783 | 0.373509 | 0.212337 |
| 8 | S9 | 22257682 | 0.747427 | 0.004869 | 0.521622 | 0.063566 | 0.334294 | 0.240641 |
| 9 | S10 | 29436289 | 0.748795 | 0.005499 | 0.560454 | 0.036219 | 0.306729 | 0.187479 |
| 10 | S11 | 31130278 | 0.741882 | 0.002740 | 0.558882 | 0.049581 | 0.349191 | 0.211787 |
| 11 | S12 | 21161595 | 0.750782 | 0.006837 | 0.756339 | 0.013878 | 0.324264 | 0.195430 |
| 12 | S13 | 28612833 | 0.733976 | 0.011718 | 0.598687 | 0.035392 | 0.357447 | 0.198566 |
| 13 | S14 | 26351189 | 0.748323 | 0.004106 | 0.517518 | 0.070293 | 0.381095 | 0.259122 |
| 14 | S15 | 25739575 | 0.748421 | 0.003353 | 0.526238 | 0.050938 | 0.324207 | 0.212366 |
| 15 | S16 | 26802346 | 0.739833 | 0.009370 | 0.520287 | 0.071503 | 0.358758 | 0.240009 |
| 16 | S17 | 26343522 | 0.749358 | 0.003155 | 0.673195 | 0.024121 | 0.301588 | 0.245854 |
| 17 | S18 | 25290073 | 0.749358 | 0.007465 | 0.562382 | 0.048528 | 0.314776 | 0.215160 |
| 18 | 10k_rep1 | 28247826 | 0.688553 | 0.018993 | 0.547000 | 0.056113 | 0.484393 | 0.140333 |
| 19 | 10k_rep2 | 39303876 | 0.690313 | 0.017328 | 0.547621 | 0.055600 | 0.474634 | 0.142889 |
| 20 | 10k_rep3 | 29831281 | 0.710875 | 0.010610 | 0.518053 | 0.066053 | 0.488738 | 0.168180 |
| 21 | MB_SC1 | 13848219 | 0.545000 | 0.007000 | 0.531495 | 0.127934 | 0.207841 | 0.728980 |
| 22 | MB_SC2 | 13550218 | 0.458000 | 0.010800 | 0.569271 | 0.102581 | 0.179407 | 0.694747 |
| 23 | MB_SC3 | 26765848 | 0.496000 | 0.007900 | 0.535192 | 0.141893 | 0.231068 | 0.722080 |
Create a flotilla Study!¶
study = flotilla.Study(# The metadata describing phenotype and pooled samples
metadata,
# A version for this data
version='0.1.0',
# Dataframe of the filtered expression data
expression_data=expression_filtered,
# Dataframe of the feature data of the genes
expression_feature_data=expression_feature_data,
# Dataframe of the splicing data
splicing_data=splicing,
# Dataframe of the feature data of the splicing events
splicing_feature_data=splicing_feature_data,
# Specify "gene_name" as the column we want to rename the splicing ids to
splicing_feature_rename_col="gene_name",
# Specify "gene_name" as the column that links splicing ids to expression ids
splicing_feature_expression_id_col="gene_name",
# Dataframe of the mapping stats data
mapping_stats_data=mapping_stats,
# Which column in "mapping_stats" has the number of reads
mapping_stats_number_mapped_col='PF_READS')
2014-12-10 15:36:38 Initializing Study
2014-12-10 15:36:38 Initializing Predictor configuration manager for Study
2014-12-10 15:36:38 Predictor ExtraTreesClassifier is of type <class 'sklearn.ensemble.forest.ExtraTreesClassifier'>
2014-12-10 15:36:38 Added ExtraTreesClassifier to default predictors
2014-12-10 15:36:38 Predictor ExtraTreesRegressor is of type <class 'sklearn.ensemble.forest.ExtraTreesRegressor'>
2014-12-10 15:36:38 Added ExtraTreesRegressor to default predictors
2014-12-10 15:36:38 Predictor GradientBoostingClassifier is of type <class 'sklearn.ensemble.gradient_boosting.GradientBoostingClassifier'>
2014-12-10 15:36:38 Added GradientBoostingClassifier to default predictors
2014-12-10 15:36:38 Predictor GradientBoostingRegressor is of type <class 'sklearn.ensemble.gradient_boosting.GradientBoostingRegressor'>
2014-12-10 15:36:38 Added GradientBoostingRegressor to default predictors
2014-12-10 15:36:38 Loading metadata
2014-12-10 15:36:38 Loading expression data
2014-12-10 15:36:38 Initializing expression
2014-12-10 15:36:38 Done initializing expression
2014-12-10 15:36:38 Loading splicing data
2014-12-10 15:36:38 Initializing splicing
2014-12-10 15:36:38 Done initializing splicing
2014-12-10 15:36:38 Successfully initialized a Study object!
No phenotype to color mapping was provided, so coming up with reasonable defaults
No phenotype to marker (matplotlib plotting symbol) was provided, so each phenotype will be plotted as a circle in the PCA visualizations.
As a side note, you can save this study to disk now, so you can “embark” later:
study.save('shalek2013')
Wrote datapackage to /Users/olga/flotilla_projects/shalek2013/datapackage.json
Note that this is saved to my home directory, in ~/flotilla_projects/<study_name>/ (the “~” stands for my “home directory”, in this case /Users/olga). This will be saved in your home directory, too.
The datapackage.json file is what holds all the information relative to the study, and loosely follows the datapackage spec created by the Open Knowledge Foundation.
cat /Users/olga/flotilla_projects/shalek2013/datapackage.json
{
"name": "shalek2013",
"title": null,
"datapackage_version": "0.1.1",
"sources": null,
"licenses": null,
"resources": [
{
"path": "splicing.csv.gz",
"format": "csv",
"name": "splicing",
"compression": "gzip"
},
{
"number_mapped_col": "PF_READS",
"path": "mapping_stats.csv.gz",
"format": "csv",
"name": "mapping_stats",
"compression": "gzip"
},
{
"name": "expression_feature",
"format": "csv",
"rename_col": null,
"ignore_subset_cols": [],
"path": "expression_feature.csv.gz",
"compression": "gzip"
},
{
"name": "expression",
"log_base": null,
"format": "csv",
"thresh": -Infinity,
"plus_one": false,
"path": "expression.csv.gz",
"compression": "gzip"
},
{
"name": "splicing_feature",
"format": "csv",
"rename_col": "gene_name",
"ignore_subset_cols": [],
"path": "splicing_feature.csv.gz",
"expression_id_col": "gene_name",
"compression": "gzip"
},
{
"pooled_col": "pooled",
"name": "metadata",
"phenotype_to_marker": {
"BDMC": "o"
},
"format": "csv",
"minimum_samples": 0,
"phenotype_to_color": {
"BDMC": "#1b9e77"
},
"path": "metadata.csv.gz",
"phenotype_col": "phenotype",
"phenotype_order": [
"BDMC"
],
"compression": "gzip"
}
]
}
One thing to note is that when you save, the version number is bumped up. study.version (the one we just made) is 0.1.0, but the one we saved is 0.1.1, since we could have made some changes to the data.
Let’s look at what else is in this folder:
ls /Users/olga/flotilla_projects/shalek2013
datapackage.json expression_feature.csv mapping_stats.csv.gz splicing.csv splicing_feature.csv.gz
expression.csv expression_feature.csv.gz metadata.csv splicing.csv.gz
expression.csv.gz mapping_stats.csv metadata.csv.gz splicing_feature.csv
So this is where all the other files are. Good to know!
We can “embark” on this newly-saved study now very painlessly, without having to open and process all those files again:
study2 = flotilla.embark('shalek2013')
2014-12-10 15:34:27 Reading datapackage from /Users/olga/flotilla_projects/shalek2013/datapackage.json
2014-12-10 15:34:27 Parsing datapackage to create a Study object
2014-12-10 15:34:27 Initializing Study
2014-12-10 15:34:27 Initializing Predictor configuration manager for Study
2014-12-10 15:34:27 Predictor ExtraTreesClassifier is of type <class 'sklearn.ensemble.forest.ExtraTreesClassifier'>
2014-12-10 15:34:27 Added ExtraTreesClassifier to default predictors
2014-12-10 15:34:27 Predictor ExtraTreesRegressor is of type <class 'sklearn.ensemble.forest.ExtraTreesRegressor'>
2014-12-10 15:34:27 Added ExtraTreesRegressor to default predictors
2014-12-10 15:34:27 Predictor GradientBoostingClassifier is of type <class 'sklearn.ensemble.gradient_boosting.GradientBoostingClassifier'>
2014-12-10 15:34:27 Added GradientBoostingClassifier to default predictors
2014-12-10 15:34:27 Predictor GradientBoostingRegressor is of type <class 'sklearn.ensemble.gradient_boosting.GradientBoostingRegressor'>
2014-12-10 15:34:27 Added GradientBoostingRegressor to default predictors
2014-12-10 15:34:27 Loading metadata
2014-12-10 15:34:27 Loading expression data
2014-12-10 15:34:27 Initializing expression
2014-12-10 15:34:27 Done initializing expression
2014-12-10 15:34:27 Loading splicing data
2014-12-10 15:34:27 Initializing splicing
2014-12-10 15:34:27 Done initializing splicing
2014-12-10 15:34:27 Successfully initialized a Study object!
Now we can start creating figures!
Figure 1¶
Here, we will attempt to re-create the sub-panels in Figure 1, where the original is:

Original Figure 1
Figure 1a¶
study.plot_two_samples('P1', 'P2')
/usr/local/lib/python2.7/site-packages/matplotlib/figure.py:1644: UserWarning: This figure includes Axes that are not compatible with tight_layout, so its results might be incorrect.
warnings.warn("This figure includes Axes that are not "
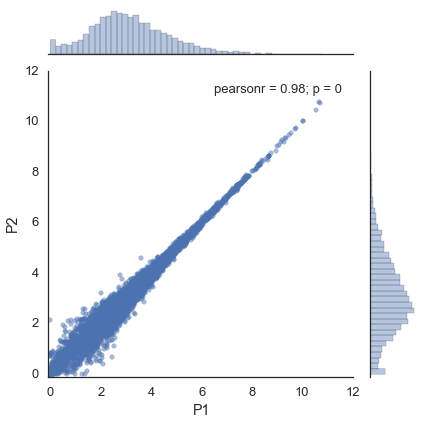
Without flotilla, you would do¶
import seaborn as sns
sns.set_style('ticks')
x = expression_filtered.ix['P1']
y = expression_filtered.ix['P2']
jointgrid = sns.jointplot(x, y, joint_kws=dict(alpha=0.5))
xmin, xmax, ymin, ymax = jointgrid.ax_joint.axis()
jointgrid.ax_joint.set_xlim(0, xmax)
jointgrid.ax_joint.set_ylim(0, ymax);
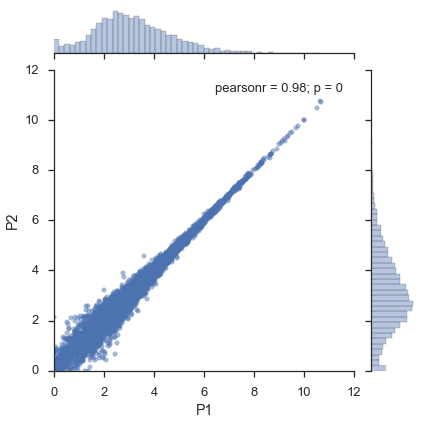
Figure 1b¶
Paper: \(r=0.54\). Not sure at all what’s going on here.
study.plot_two_samples('S1', 'S2')
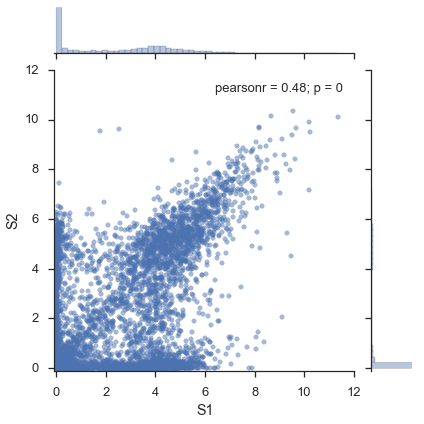
Without flotilla¶
import seaborn as sns
sns.set_style('ticks')
x = expression_filtered.ix['S1']
y = expression_filtered.ix['S2']
jointgrid = sns.jointplot(x, y, joint_kws=dict(alpha=0.5))
# Adjust xmin, ymin to 0
xmin, xmax, ymin, ymax = jointgrid.ax_joint.axis()
jointgrid.ax_joint.set_xlim(0, xmax)
jointgrid.ax_joint.set_ylim(0, ymax);
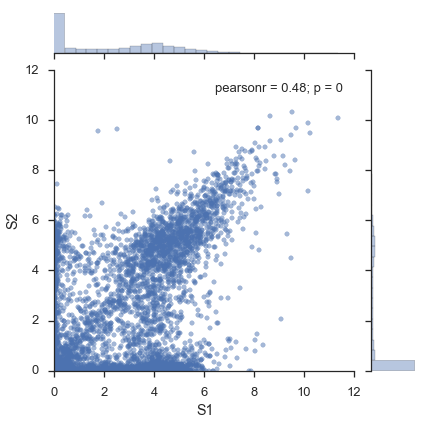
By the way, you can do other kinds of plots with flotilla, like a kernel density estimate (“kde”) plot:
study.plot_two_samples('S1', 'S2', kind='kde')
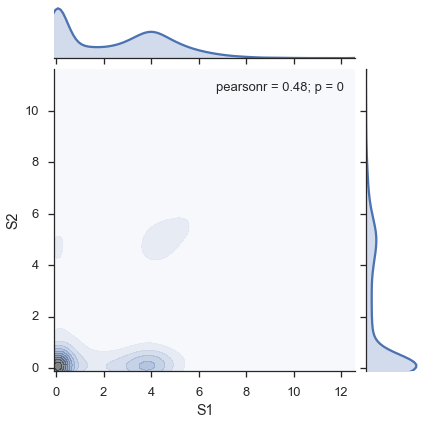
Or a binned hexagon plot (“hexbin"):
study.plot_two_samples('S1', 'S2', kind='hexbin')
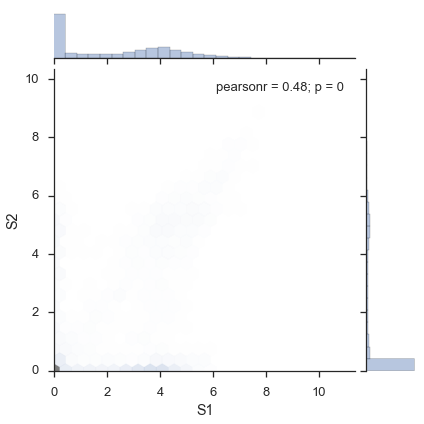
Any inputs that are valid to seaborn‘s `jointplot <http://web.stanford.edu/~mwaskom/software/seaborn/generated/seaborn.jointplot.html#seaborn.jointplot>`_ are valid.
Figure 1c¶
x = study.expression.data.ix['P1']
y = study.expression.singles.mean()
y.name = "Average singles"
jointgrid = sns.jointplot(x, y, joint_kws=dict(alpha=0.5))
# Adjust xmin, ymin to 0
xmin, xmax, ymin, ymax = jointgrid.ax_joint.axis()
jointgrid.ax_joint.set_xlim(0, xmax)
jointgrid.ax_joint.set_ylim(0, ymax);
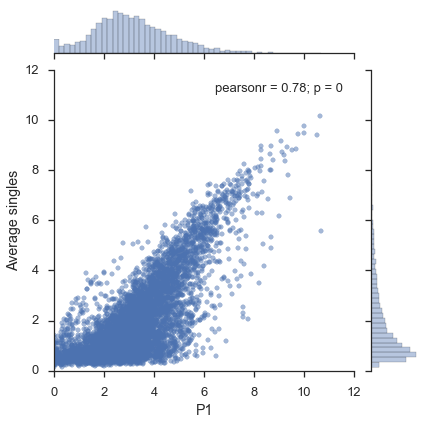
Figure 2¶
Next, we will attempt to recreate the figures from Figure 2:

Original figure 2
Figure 2a¶
For this figure, we will need the “LPS Response” and “Housekeeping” gene annotations, from the expression_feature_data that we created.
# Get colors for plotting the gene categories
dark2 = sns.color_palette('Dark2')
singles = study.expression.singles
# Get only gene categories for genes in the singles data
singles, gene_categories = singles.align(study.expression.feature_data.gene_category, join='left', axis=1)
mean = singles.mean()
std = singles.std()
jointgrid = sns.jointplot(mean, std, color='#262626', joint_kws=dict(alpha=0.5))
for i, (category, s) in enumerate(gene_categories.groupby(gene_categories)):
jointgrid.ax_joint.plot(mean[s.index], std[s.index], 'o', color=dark2[i], markersize=5)
jointgrid.ax_joint.set_xlabel('Standard deviation in single cells $\mu$')
jointgrid.ax_joint.set_ylabel('Average expression in single cells $\sigma$')
xmin, xmax, ymin, ymax = jointgrid.ax_joint.axis()
vmax = max(xmax, ymax)
vmin = min(xmin, ymin)
jointgrid.ax_joint.plot([0, vmax], [0, vmax], color='steelblue')
jointgrid.ax_joint.plot([0, vmax], [0, .25*vmax], color='grey')
jointgrid.ax_joint.set_xlim(0, xmax)
jointgrid.ax_joint.set_ylim(0, ymax)
jointgrid.ax_joint.fill_betweenx((ymin, ymax), 0, np.log(250), alpha=0.5, zorder=-1);
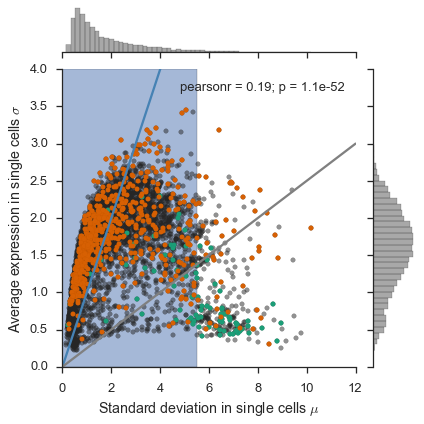
I couldn’t find the data for the ``hESC``s for the right-side panel of Fig. 2a, so I couldn’t remake the figure.
Figure 2b¶
In the paper, they use “522 most highly expressed genes (single-cell average TPM > 250)”, but I wasn’t able to replicate their numbers. If I use the pre-filtered expression data that I fed into flotilla, then I get 297 genes:
mean = study.expression.singles.mean()
highly_expressed_genes = mean.index[mean > np.log(250 + 1)]
len(highly_expressed_genes)
297
Which is much less. If I use the original, unfiltered data, then I get the “522” number, but this seems strange because they did the filtering step of “discarded genes not appreciably expressed (transcripts per million (TPM) > 1) in at least three individual cells, retaining 6,313 genes for further analysis”, and yet they went back to the original data to get this new subset.
expression.ix[:, expression.ix[singles_ids].mean() > 250].shape
(21, 522)
expression_highly_expressed = np.log(expression.ix[singles_ids, expression.ix[singles_ids].mean() > 250] + 1)
mean = expression_highly_expressed.mean()
std = expression_highly_expressed.std()
mean_bins = pd.cut(mean, bins=np.arange(0, 11, 1))
# Coefficient of variation
cv = std/mean
cv.sort()
genes = mean.index
# for name, df in shalek2013.expression.singles.groupby(dict(zip(genes, mean_bins)), axis=1):
def calculate_cells_per_tpm_per_cv(df, cv):
df = df[df > 1]
df_aligned, cv_aligned = df.align(cv, join='inner', axis=1)
cv_aligned.sort()
n_cells = pd.Series(0, index=cv.index)
n_cells[cv_aligned.index] = df_aligned.ix[:, cv_aligned.index].count()
return n_cells
grouped = expression_highly_expressed.groupby(dict(zip(genes, mean_bins)), axis=1)
cells_per_tpm_per_cv = grouped.apply(calculate_cells_per_tpm_per_cv, cv=cv)
Here’s how you would make the original figure from the paper:
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(10, 10))
sns.heatmap(cells_per_tpm_per_cv, linewidth=0, ax=ax, yticklabels=False)
ax.set_yticks([])
ax.set_xlabel('ln(TPM, binned)');
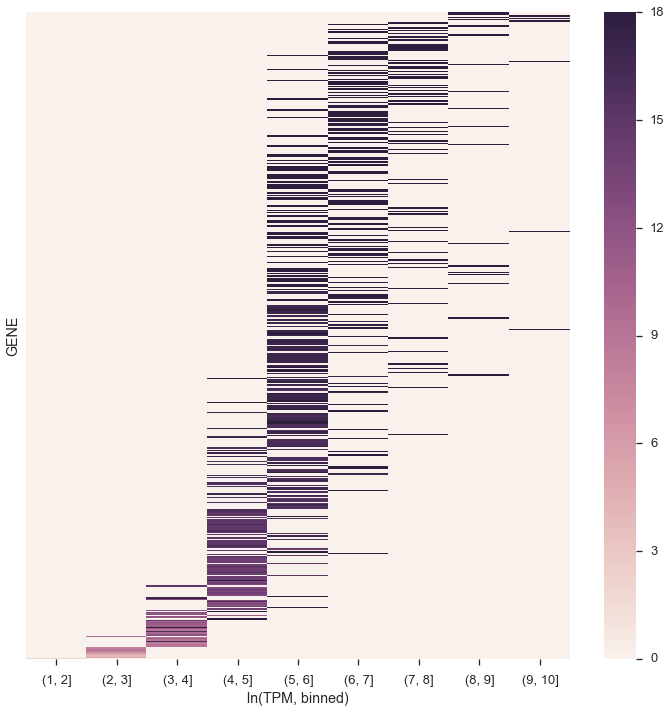
Doesn’t quite look the same. Maybe the y-axis labels were opposite, and higher up on the y-axis was less variant? Because I see a blob of color for (1,2] TPM (by the way, the figure in the paper is not TPM+1 as previous figures were)
This is how you would make a modified version of the figure, which also plots the coefficient of variation on a side-plot, which I like because it shows the CV changes directly on the heatmap. Also, technically this is \(\ln\)(TPM+1).
from matplotlib import gridspec
fig = plt.figure(figsize=(12, 10))
gs = gridspec.GridSpec(1, 2, wspace=0.01, hspace=0.01, width_ratios=[.2, 1])
cv_ax = fig.add_subplot(gs[0, 0])
heatmap_ax = fig.add_subplot(gs[0, 1])
sns.heatmap(cells_per_tpm_per_cv, linewidth=0, ax=heatmap_ax)
heatmap_ax.set_yticks([])
heatmap_ax.set_xlabel('$\ln$(TPM+1), binned')
y = np.arange(cv.shape[0])
cv_ax.set_xscale('log')
cv_ax.plot(cv, y, color='#262626')
cv_ax.fill_betweenx(cv, np.zeros(cv.shape), y, color='#262626', alpha=0.5)
cv_ax.set_ylim(0, y.max())
cv_ax.set_xlabel('CV = $\mu/\sigma$')
cv_ax.set_yticks([])
sns.despine(ax=cv_ax, left=True, right=False)
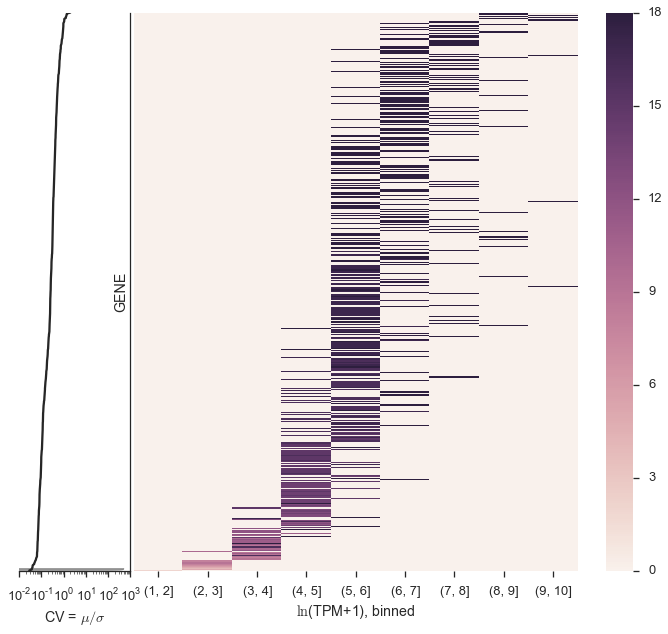
Figure 3¶
We will attempt to re-create the sub-panel figures from Figure 3:

Original Figure 3
Since we can’t re-do the microscopy (Figure 3a) or the RNA-FISH counts (Figure 3c), we will make Figures 3b. These histograms are simple to do outside of flotilla, so we do not have them within flotilla.
Figure 3b, top panel¶
fig, ax = plt.subplots()
sns.distplot(study.splicing.singles.values.flat, bins=np.arange(0, 1.05, 0.05), ax=ax)
ax.set_xlim(0, 1)
sns.despine()
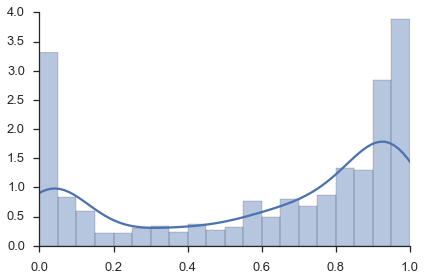
Figure 3b, bottom panel¶
fig, ax = plt.subplots()
sns.distplot(study.splicing.pooled.values.flat, bins=np.arange(0, 1.05, 0.05), ax=ax, color='grey')
ax.set_xlim(0, 1)
sns.despine()
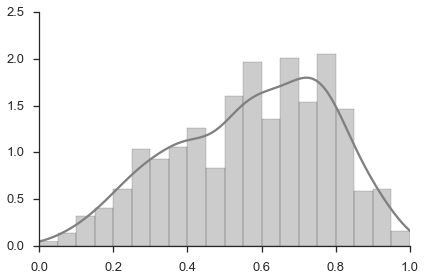
Figure 4¶
We will attempt to re-create the sub-panel figures from Figure 4:

Original Figure 4
Figure 4a¶
Here, we can use the “interactive_pca” function we have to explore different dimensionality reductions on the data.
study.interactive_pca()
featurewise : False
y_pc : 2
data_type : expression
show_point_labels : False
sample_subset : all_samples
feature_subset : variant
plot_violins : False
x_pc : 1
list_link :
<function flotilla.visualize.ipython_interact.do_interact>
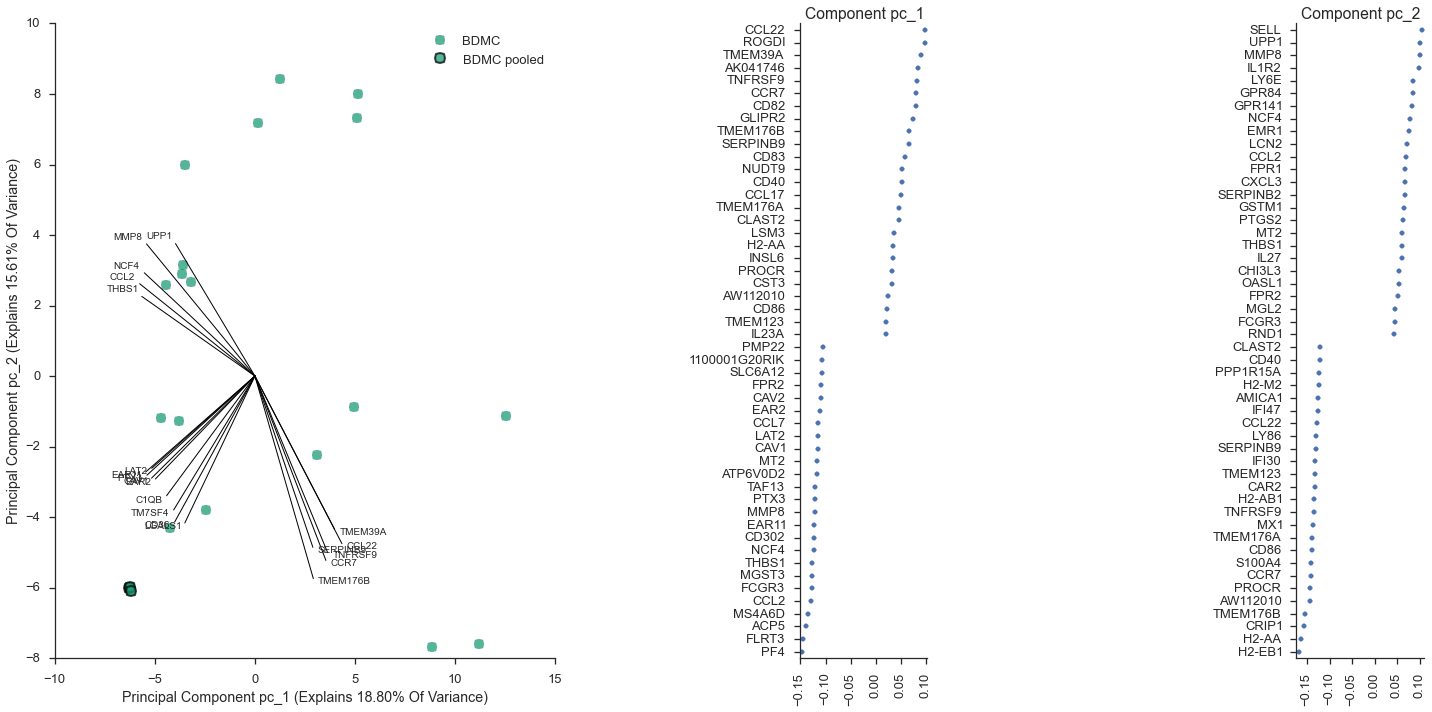
A “sequences shortened” version of this is available as a gif:

Imgur
Equivalently, I could have written out the plotting command by hand, instead of using study.interactive_pca:
study.plot_pca(feature_subset='gene_category: LPS Response', sample_subset='not (pooled)', plot_violins=False, show_point_labels=True)
<flotilla.visualize.decomposition.DecompositionViz at 0x1125d52d0>
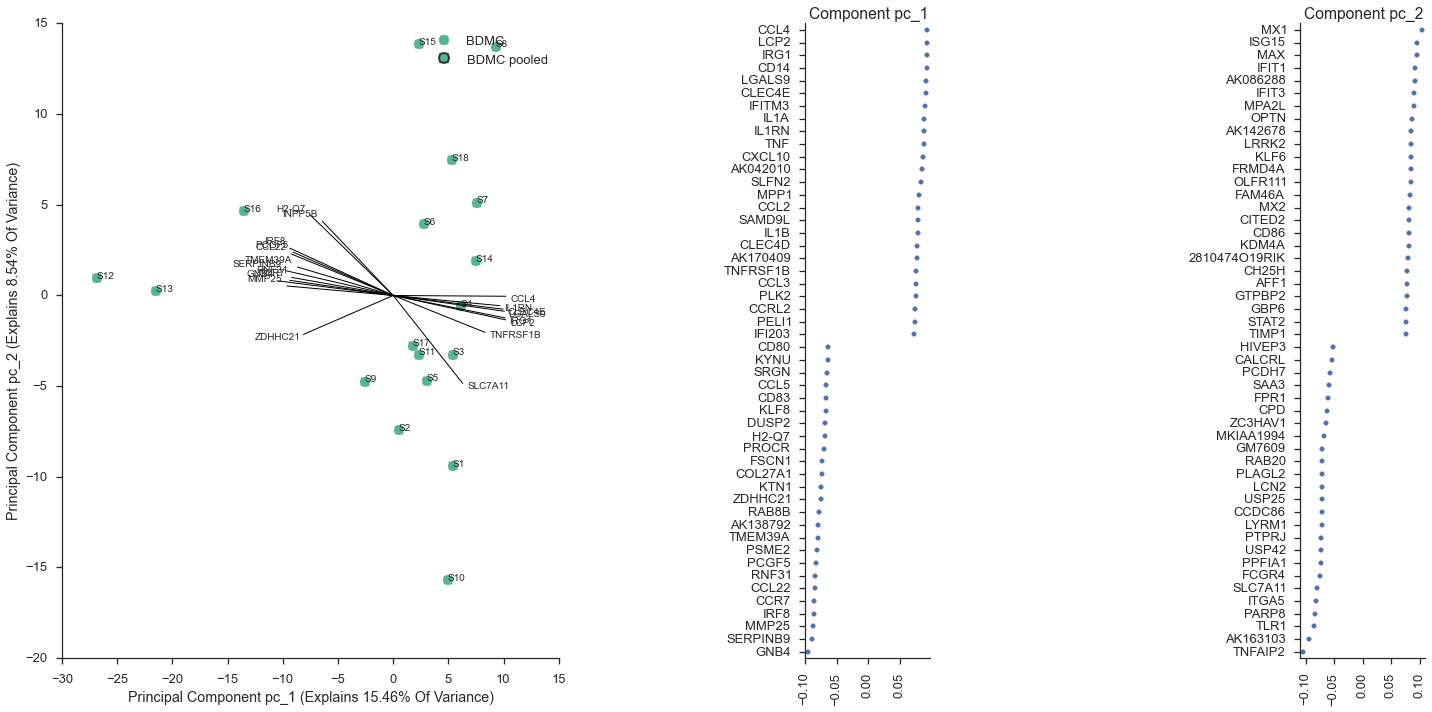
Mark immature cells as a new subset¶
As in the paper, the cells S12, S13, and S16 appear in a cluster that is separate from the remaining cells. From the paper, these were the “matured” bone-marrow derived dendritic cells, after stimulation with a lipopolysaccharide. We can mark these as mature in our metadata,
mature = ['S12', 'S13', 'S16']
study.metadata.data['maturity'] = metadata.index.map(lambda x: 'mature' if x in mature else 'immature')
study.metadata.data.head()
| phenotype | pooled | outlier | maturity | |
|---|---|---|---|---|
| S1 | BDMC | False | False | immature |
| S2 | BDMC | False | False | immature |
| S3 | BDMC | False | False | immature |
| S4 | BDMC | False | False | immature |
| S5 | BDMC | False | False | immature |
Then, we can set maturity as the column we use for coloring the PCA, since before it was the “phenotype” column.
study.metadata.phenotype_col = 'maturity'
study.save('shalek2013')
study = flotilla.embark('shalek2013')
Wrote datapackage to /Users/olga/flotilla_projects/shalek2013/datapackage.json2014-12-10 15:41:07 Reading datapackage from /Users/olga/flotilla_projects/shalek2013/datapackage.json
2014-12-10 15:41:07 Parsing datapackage to create a Study object
2014-12-10 15:41:07 Initializing Study
2014-12-10 15:41:07 Initializing Predictor configuration manager for Study
2014-12-10 15:41:07 Predictor ExtraTreesClassifier is of type <class 'sklearn.ensemble.forest.ExtraTreesClassifier'>
2014-12-10 15:41:07 Added ExtraTreesClassifier to default predictors
2014-12-10 15:41:07 Predictor ExtraTreesRegressor is of type <class 'sklearn.ensemble.forest.ExtraTreesRegressor'>
2014-12-10 15:41:07 Added ExtraTreesRegressor to default predictors
2014-12-10 15:41:07 Predictor GradientBoostingClassifier is of type <class 'sklearn.ensemble.gradient_boosting.GradientBoostingClassifier'>
2014-12-10 15:41:07 Added GradientBoostingClassifier to default predictors
2014-12-10 15:41:07 Predictor GradientBoostingRegressor is of type <class 'sklearn.ensemble.gradient_boosting.GradientBoostingRegressor'>
2014-12-10 15:41:07 Added GradientBoostingRegressor to default predictors
2014-12-10 15:41:07 Loading metadata
2014-12-10 15:41:07 Loading expression data
2014-12-10 15:41:07 Initializing expression
2014-12-10 15:41:07 Done initializing expression
2014-12-10 15:41:07 Loading splicing data
2014-12-10 15:41:07 Initializing splicing
2014-12-10 15:41:07 Done initializing splicing
2014-12-10 15:41:07 Successfully initialized a Study object!
No color was assigned to the phenotype immature, assigning a random colorNo color was assigned to the phenotype mature, assigning a random colorimmature does not have marker style, falling back on "o" (circle)mature does not have marker style, falling back on "o" (circle)
study.plot_pca(feature_subset='gene_category: LPS Response', sample_subset='not (pooled)', plot_violins=False, show_point_labels=True)
<flotilla.visualize.decomposition.DecompositionViz at 0x118468090>
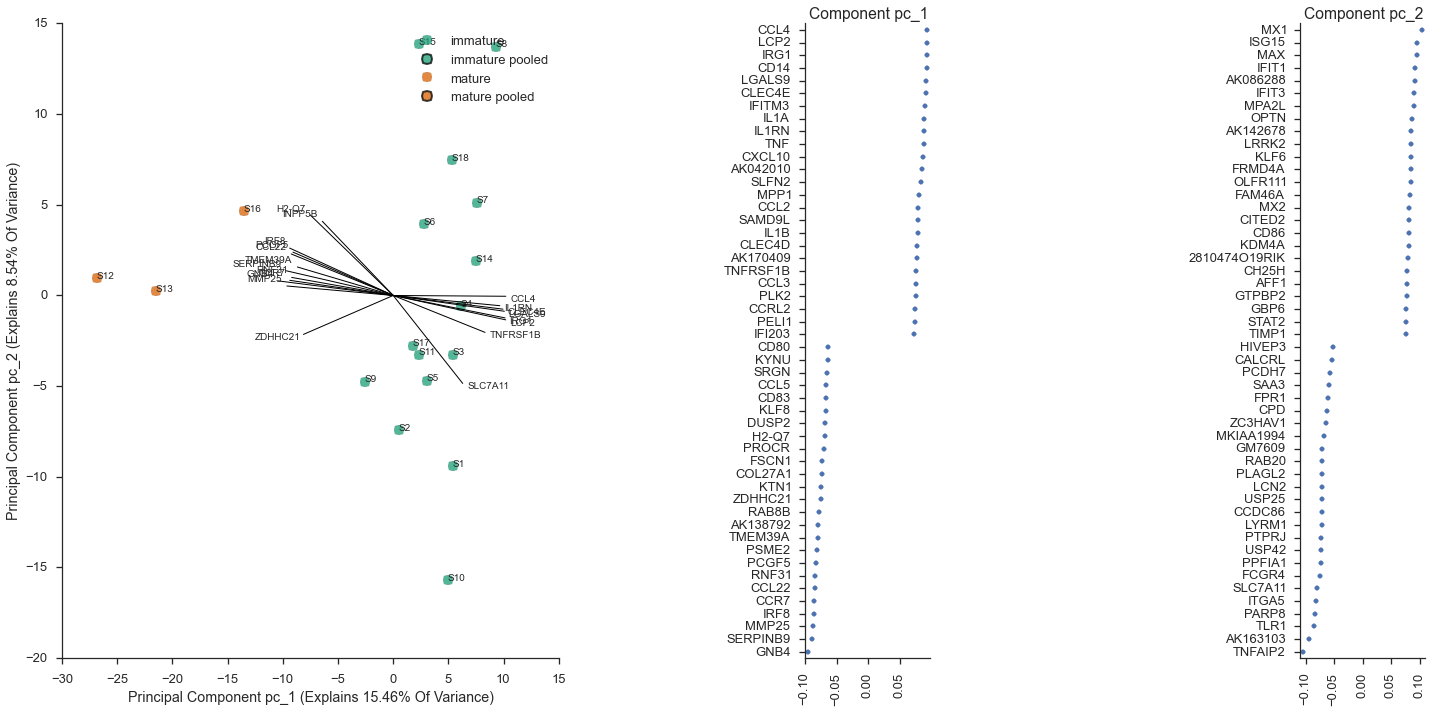
study.save('shalek2013')
Wrote datapackage to /Users/olga/flotilla_projects/shalek2013/datapackage.json
Without flotilla, plot_pca is quite a bit of code:
import sys
from collections import defaultdict
from itertools import cycle
import math
from sklearn import decomposition
from sklearn.preprocessing import StandardScaler
import pandas as pd
from matplotlib.gridspec import GridSpec, GridSpecFromSubplotSpec
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from flotilla.visualize.color import dark2
from flotilla.visualize.generic import violinplot
class DataFrameReducerBase(object):
"""
Just like scikit-learn's reducers, but with prettied up DataFrames.
"""
def __init__(self, df, n_components=None, **decomposer_kwargs):
# This magically initializes the reducer like DataFramePCA or DataFrameNMF
if df.shape[1] <= 3:
raise ValueError(
"Too few features (n={}) to reduce".format(df.shape[1]))
super(DataFrameReducerBase, self).__init__(n_components=n_components,
**decomposer_kwargs)
self.reduced_space = self.fit_transform(df)
def relabel_pcs(self, x):
return "pc_" + str(int(x) + 1)
def fit(self, X):
try:
assert type(X) == pd.DataFrame
except AssertionError:
sys.stdout.write("Try again as a pandas DataFrame")
raise ValueError('Input X was not a pandas DataFrame, '
'was of type {} instead'.format(str(type(X))))
self.X = X
super(DataFrameReducerBase, self).fit(X)
self.components_ = pd.DataFrame(self.components_,
columns=self.X.columns).rename_axis(
self.relabel_pcs, 0)
try:
self.explained_variance_ = pd.Series(
self.explained_variance_).rename_axis(self.relabel_pcs, 0)
self.explained_variance_ratio_ = pd.Series(
self.explained_variance_ratio_).rename_axis(self.relabel_pcs,
0)
except AttributeError:
pass
return self
def transform(self, X):
component_space = super(DataFrameReducerBase, self).transform(X)
if type(self.X) == pd.DataFrame:
component_space = pd.DataFrame(component_space,
index=X.index).rename_axis(
self.relabel_pcs, 1)
return component_space
def fit_transform(self, X):
try:
assert type(X) == pd.DataFrame
except:
sys.stdout.write("Try again as a pandas DataFrame")
raise ValueError('Input X was not a pandas DataFrame, '
'was of type {} instead'.format(str(type(X))))
self.fit(X)
return self.transform(X)
class DataFramePCA(DataFrameReducerBase, decomposition.PCA):
pass
class DataFrameNMF(DataFrameReducerBase, decomposition.NMF):
def fit(self, X):
"""
duplicated fit code for DataFrameNMF because sklearn's NMF cheats for
efficiency and calls fit_transform. MRO resolves the closest
(in this package)
_single_fit_transform first and so there's a recursion error:
def fit(self, X, y=None, **params):
self._single_fit_transform(X, **params)
return self
"""
try:
assert type(X) == pd.DataFrame
except:
sys.stdout.write("Try again as a pandas DataFrame")
raise ValueError('Input X was not a pandas DataFrame, '
'was of type {} instead'.format(str(type(X))))
self.X = X
# notice this is fit_transform, not fit
super(decomposition.NMF, self).fit_transform(X)
self.components_ = pd.DataFrame(self.components_,
columns=self.X.columns).rename_axis(
self.relabel_pcs, 0)
return self
class DataFrameICA(DataFrameReducerBase, decomposition.FastICA):
pass
class DecompositionViz(object):
"""
Plots the reduced space from a decomposed dataset. Does not perform any
reductions of its own
"""
def __init__(self, reduced_space, components_,
explained_variance_ratio_,
feature_renamer=None, groupby=None,
singles=None, pooled=None, outliers=None,
featurewise=False,
order=None, violinplot_kws=None,
data_type='expression', label_to_color=None,
label_to_marker=None,
scale_by_variance=True, x_pc='pc_1',
y_pc='pc_2', n_vectors=20, distance='L1',
n_top_pc_features=50, max_char_width=30):
"""Plot the results of a decomposition visualization
Parameters
----------
reduced_space : pandas.DataFrame
A (n_samples, n_dimensions) DataFrame of the post-dimensionality
reduction data
components_ : pandas.DataFrame
A (n_features, n_dimensions) DataFrame of how much each feature
contributes to the components (trailing underscore to be
consistent with scikit-learn)
explained_variance_ratio_ : pandas.Series
A (n_dimensions,) Series of how much variance each component
explains. (trailing underscore to be consistent with scikit-learn)
feature_renamer : function, optional
A function which takes the name of the feature and renames it,
e.g. from an ENSEMBL ID to a HUGO known gene symbol. If not
provided, the original name is used.
groupby : mapping function | dict, optional
A mapping of the samples to a label, e.g. sample IDs to
phenotype, for the violinplots. If None, all samples are treated
the same and are colored the same.
singles : pandas.DataFrame, optional
For violinplots only. If provided and 'plot_violins' is True,
will plot the raw (not reduced) measurement values as violin plots.
pooled : pandas.DataFrame, optional
For violinplots only. If provided, pooled samples are plotted as
black dots within their label.
outliers : pandas.DataFrame, optional
For violinplots only. If provided, outlier samples are plotted as
a grey shadow within their label.
featurewise : bool, optional
If True, then the "samples" are features, e.g. genes instead of
samples, and the "features" are the samples, e.g. the cells
instead of the gene ids. Essentially, the transpose of the
original matrix. If True, then violins aren't plotted. (default
False)
order : list-like
The order of the labels for the violinplots, e.g. if the data is
from a differentiation timecourse, then this would be the labels
of the phenotypes, in the differentiation order.
violinplot_kws : dict
Any additional parameters to violinplot
data_type : 'expression' | 'splicing', optional
For violinplots only. The kind of data that was originally used
for the reduction. (default 'expression')
label_to_color : dict, optional
A mapping of the label, e.g. the phenotype, to the desired
plotting color (default None, auto-assigned with the groupby)
label_to_marker : dict, optional
A mapping of the label, e.g. the phenotype, to the desired
plotting symbol (default None, auto-assigned with the groupby)
scale_by_variance : bool, optional
If True, scale the x- and y-axes by their explained_variance_ratio_
(default True)
{x,y}_pc : str, optional
Principal component to plot on the x- and y-axis. (default "pc_1"
and "pc_2")
n_vectors : int, optional
Number of vectors to plot of the principal components. (default 20)
distance : 'L1' | 'L2', optional
The distance metric to use to plot the vector lengths. L1 is
"Cityblock", i.e. the sum of the x and y coordinates, and L2 is
the traditional Euclidean distance. (default "L1")
n_top_pc_features : int, optional
THe number of top features from the principal components to plot.
(default 50)
max_char_width : int, optional
Maximum character width of a feature name. Useful for crazy long
feature IDs like MISO IDs
"""
self.reduced_space = reduced_space
self.components_ = components_
self.explained_variance_ratio_ = explained_variance_ratio_
self.singles = singles
self.pooled = pooled
self.outliers = outliers
self.groupby = groupby
self.order = order
self.violinplot_kws = violinplot_kws if violinplot_kws is not None \
else {}
self.data_type = data_type
self.label_to_color = label_to_color
self.label_to_marker = label_to_marker
self.n_vectors = n_vectors
self.x_pc = x_pc
self.y_pc = y_pc
self.pcs = (self.x_pc, self.y_pc)
self.distance = distance
self.n_top_pc_features = n_top_pc_features
self.featurewise = featurewise
self.feature_renamer = feature_renamer
self.max_char_width = max_char_width
if self.label_to_color is None:
colors = cycle(dark2)
def color_factory():
return colors.next()
self.label_to_color = defaultdict(color_factory)
if self.label_to_marker is None:
markers = cycle(['o', '^', 's', 'v', '*', 'D', 'h'])
def marker_factory():
return markers.next()
self.label_to_marker = defaultdict(marker_factory)
if self.groupby is None:
self.groupby = dict.fromkeys(self.reduced_space.index, 'all')
self.grouped = self.reduced_space.groupby(self.groupby, axis=0)
if order is not None:
self.color_ordered = [self.label_to_color[x] for x in self.order]
else:
self.color_ordered = [self.label_to_color[x] for x in
self.grouped.groups]
self.loadings = self.components_.ix[[self.x_pc, self.y_pc]]
# Get the explained variance
if explained_variance_ratio_ is not None:
self.vars = explained_variance_ratio_[[self.x_pc, self.y_pc]]
else:
self.vars = pd.Series([1., 1.], index=[self.x_pc, self.y_pc])
if scale_by_variance:
self.loadings = self.loadings.multiply(self.vars, axis=0)
# sort features by magnitude/contribution to transformation
reduced_space = self.reduced_space[[self.x_pc, self.y_pc]]
farthest_sample = reduced_space.apply(np.linalg.norm, axis=0).max()
whole_space = self.loadings.apply(np.linalg.norm).max()
scale = .25 * farthest_sample / whole_space
self.loadings *= scale
ord = 2 if self.distance == 'L2' else 1
self.magnitudes = self.loadings.apply(np.linalg.norm, ord=ord)
self.magnitudes.sort(ascending=False)
self.top_features = set([])
self.pc_loadings_labels = {}
self.pc_loadings = {}
for pc in self.pcs:
x = self.components_.ix[pc].copy()
x.sort(ascending=True)
half_features = int(self.n_top_pc_features / 2)
if len(x) > self.n_top_pc_features:
a = x[:half_features]
b = x[-half_features:]
labels = np.r_[a.index, b.index]
self.pc_loadings[pc] = np.r_[a, b]
else:
labels = x.index
self.pc_loadings[pc] = x
self.pc_loadings_labels[pc] = labels
self.top_features.update(labels)
def __call__(self, ax=None, title='', plot_violins=True,
show_point_labels=False,
show_vectors=True,
show_vector_labels=True,
markersize=10, legend=True):
gs_x = 14
gs_y = 12
if ax is None:
self.reduced_fig, ax = plt.subplots(1, 1, figsize=(20, 10))
gs = GridSpec(gs_x, gs_y)
else:
gs = GridSpecFromSubplotSpec(gs_x, gs_y, ax.get_subplotspec())
self.reduced_fig = plt.gcf()
ax_components = plt.subplot(gs[:, :5])
ax_loading1 = plt.subplot(gs[:, 6:8])
ax_loading2 = plt.subplot(gs[:, 10:14])
self.plot_samples(show_point_labels=show_point_labels,
title=title, show_vectors=show_vectors,
show_vector_labels=show_vector_labels,
markersize=markersize, legend=legend,
ax=ax_components)
self.plot_loadings(pc=self.x_pc, ax=ax_loading1)
self.plot_loadings(pc=self.y_pc, ax=ax_loading2)
sns.despine()
self.reduced_fig.tight_layout()
if plot_violins and not self.featurewise and self.singles is not None:
self.plot_violins()
return self
def shorten(self, x):
if len(x) > self.max_char_width:
return '{}...'.format(x[:self.max_char_width])
else:
return x
def plot_samples(self, show_point_labels=True,
title='DataFramePCA', show_vectors=True,
show_vector_labels=True, markersize=10,
three_d=False, legend=True, ax=None):
"""
Given a pandas dataframe, performs DataFramePCA and plots the results in a
convenient single function.
Parameters
----------
groupby : groupby
How to group the samples by color/label
label_to_color : dict
Group labels to a matplotlib color E.g. if you've already chosen
specific colors to indicate a particular group. Otherwise will
auto-assign colors
label_to_marker : dict
Group labels to matplotlib marker
title : str
title of the plot
show_vectors : bool
Whether or not to draw the vectors indicating the supporting
principal components
show_vector_labels : bool
whether or not to draw the names of the vectors
show_point_labels : bool
Whether or not to label the scatter points
markersize : int
size of the scatter markers on the plot
text_group : list of str
Group names that you want labeled with text
three_d : bool
if you want hte plot in 3d (need to set up the axes beforehand)
Returns
-------
For each vector in data:
x, y, marker, distance
"""
if ax is None:
ax = plt.gca()
# Plot the samples
for name, df in self.grouped:
color = self.label_to_color[name]
marker = self.label_to_marker[name]
x = df[self.x_pc]
y = df[self.y_pc]
ax.plot(x, y, color=color, marker=marker, linestyle='None',
label=name, markersize=markersize, alpha=0.75,
markeredgewidth=.1)
try:
if not self.pooled.empty:
pooled_ids = x.index.intersection(self.pooled.index)
pooled_x, pooled_y = x[pooled_ids], y[pooled_ids]
ax.plot(pooled_x, pooled_y, 'o', color=color, marker=marker,
markeredgecolor='k', markeredgewidth=2,
label='{} pooled'.format(name),
markersize=markersize, alpha=0.75)
except AttributeError:
pass
try:
if not self.outliers.empty:
outlier_ids = x.index.intersection(self.outliers.index)
outlier_x, outlier_y = x[outlier_ids], y[outlier_ids]
ax.plot(outlier_x, outlier_y, 'o', color=color,
marker=marker,
markeredgecolor='lightgrey', markeredgewidth=5,
label='{} outlier'.format(name),
markersize=markersize, alpha=0.75)
except AttributeError:
pass
if show_point_labels:
for args in zip(x, y, df.index):
ax.text(*args)
# Plot vectors, if asked
if show_vectors:
for vector_label in self.magnitudes[:self.n_vectors].index:
x, y = self.loadings[vector_label]
ax.plot([0, x], [0, y], color='k', linewidth=1)
if show_vector_labels:
x_offset = math.copysign(5, x)
y_offset = math.copysign(5, y)
horizontalalignment = 'left' if x > 0 else 'right'
if self.feature_renamer is not None:
renamed = self.feature_renamer(vector_label)
else:
renamed = vector_label
ax.annotate(renamed, (x, y),
textcoords='offset points',
xytext=(x_offset, y_offset),
horizontalalignment=horizontalalignment)
# Label x and y axes
ax.set_xlabel(
'Principal Component {} (Explains {:.2f}% Of Variance)'.format(
str(self.x_pc), 100 * self.vars[self.x_pc]))
ax.set_ylabel(
'Principal Component {} (Explains {:.2f}% Of Variance)'.format(
str(self.y_pc), 100 * self.vars[self.y_pc]))
ax.set_title(title)
if legend:
ax.legend()
sns.despine()
def plot_loadings(self, pc='pc_1', n_features=50, ax=None):
loadings = self.pc_loadings[pc]
labels = self.pc_loadings_labels[pc]
if ax is None:
ax = plt.gca()
ax.plot(loadings, np.arange(loadings.shape[0]), 'o')
ax.set_yticks(np.arange(max(loadings.shape[0], n_features)))
ax.set_title("Component " + pc)
x_offset = max(loadings) * .05
ax.set_xlim(left=loadings.min() - x_offset,
right=loadings.max() + x_offset)
if self.feature_renamer is not None:
labels = map(self.feature_renamer, labels)
else:
labels = labels
labels = map(self.shorten, labels)
# ax.set_yticklabels(map(shorten, labels))
ax.set_yticklabels(labels)
for lab in ax.get_xticklabels():
lab.set_rotation(90)
sns.despine(ax=ax)
def plot_explained_variance(self, title="PCA explained variance"):
"""If the reducer is a form of PCA, then plot the explained variance
ratio by the components.
"""
# Plot the explained variance ratio
assert self.explained_variance_ratio_ is not None
import matplotlib.pyplot as plt
import seaborn as sns
fig, ax = plt.subplots()
ax.plot(self.explained_variance_ratio_, 'o-')
xticks = np.arange(len(self.explained_variance_ratio_))
ax.set_xticks(xticks)
ax.set_xticklabels(xticks + 1)
ax.set_xlabel('Principal component')
ax.set_ylabel('Fraction explained variance')
ax.set_title(title)
sns.despine()
def plot_violins(self):
"""Make violinplots of each feature
Must be called after plot_samples because it depends on the existence
of the "self.magnitudes" attribute.
"""
ncols = 4
nrows = 1
vector_labels = list(set(self.magnitudes[:self.n_vectors].index.union(
pd.Index(self.top_features))))
while ncols * nrows < len(vector_labels):
nrows += 1
self.violins_fig, axes = plt.subplots(nrows=nrows, ncols=ncols,
figsize=(4 * ncols, 4 * nrows))
if self.feature_renamer is not None:
renamed_vectors = map(self.feature_renamer, vector_labels)
else:
renamed_vectors = vector_labels
labels = [(y, x) for (y, x) in sorted(zip(renamed_vectors,
vector_labels))]
for (renamed, feature_id), ax in zip(labels, axes.flat):
singles = self.singles[feature_id] if self.singles is not None \
else None
pooled = self.pooled[feature_id] if self.pooled is not None else \
None
outliers = self.outliers[feature_id] if self.outliers is not None \
else None
title = '{}\n{}'.format(feature_id, renamed)
violinplot(singles, pooled_data=pooled, outliers=outliers,
groupby=self.groupby, color_ordered=self.color_ordered,
order=self.order, title=title,
ax=ax, data_type=self.data_type,
**self.violinplot_kws)
# Clear any unused axes
for ax in axes.flat:
# Check if the plotting space is empty
if len(ax.collections) == 0 or len(ax.lines) == 0:
ax.axis('off')
self.violins_fig.tight_layout()
# Notice we're using the original data, nothing from "study"
lps_response_genes = expression_feature_data.index[expression_feature_data.gene_category == 'LPS Response']
subset = expression_filtered.ix[singles_ids, lps_response_genes].dropna(how='all', axis=1)
subset_standardized = pd.DataFrame(StandardScaler().fit_transform(subset),
index=subset.index, columns=subset.columns)
pca = DataFramePCA(subset_standardized)
visualizer = DecompositionViz(pca.reduced_space, pca.components_, pca.explained_variance_ratio_)
visualizer();
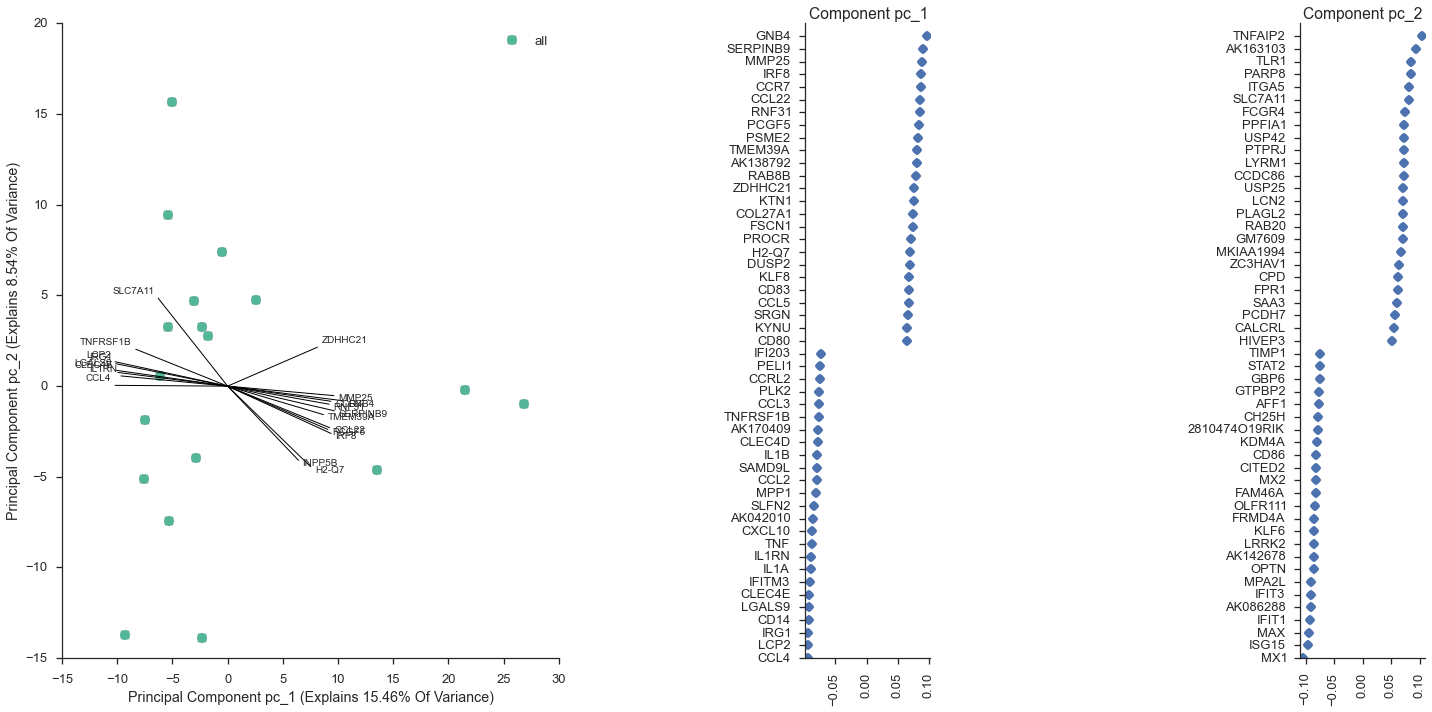
Figure 4b¶
lps_response_genes = study.expression.feature_subsets['gene_category: LPS Response']
lps_response = study.expression.singles.ix[:, lps_response_genes].dropna(how='all', axis=1)
lps_response.head()
| GENE | 1110018G07RIK | 1110038F14RIK | 1200009I06RIK | 1600014C10RIK | 1810029B16RIK | 2210009G21RIK | 2810474O19RIK | 3110001I22RIK | 4921513D23RIK | 4930523C07RIK | ... | ZC3H12C | ZC3HAV1 | ZCCHC2 | ZCCHC6 | ZDHHC21 | ZFP36 | ZFP800 | ZHX2 | ZNFX1 | ZUFSP |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S1 | 3.711442 | 0.000000 | 3.275468 | 0.000000 | 5.609305 | 0 | 0.000000 | 3.828860 | 1.314573 | 3.778275 | ... | 3.972904 | 3.509979 | 0.035344 | 3.042277 | 4.425735 | 4.092559 | 4.025124 | 0.779382 | 2.998800 | 0.000000 |
| S2 | 4.361671 | 0.147643 | 0.000000 | 0.000000 | 5.478071 | 0 | 3.407342 | 0.000000 | 1.531443 | 0.000000 | ... | 4.794306 | 4.984262 | 2.251330 | 1.018315 | 4.955713 | 0.356008 | 4.297776 | 0.032569 | 3.091207 | 5.000843 |
| S3 | 0.000000 | 3.737014 | 2.987093 | 0.063526 | 5.320993 | 0 | 3.372359 | 0.058163 | 1.105115 | 0.025043 | ... | 4.882749 | 0.807258 | 0.094925 | 0.126673 | 3.952273 | 1.956983 | 0.000000 | 0.000000 | 3.794063 | 2.928699 |
| S4 | 2.719587 | 0.000000 | 0.045823 | 0.000000 | 0.488049 | 0 | 5.127847 | 0.000000 | 2.303969 | 0.000000 | ... | 4.833354 | 4.538699 | 0.137427 | 2.025546 | 4.193989 | 2.372572 | 0.121924 | 0.000000 | 0.230278 | 0.430168 |
| S5 | 2.982073 | 0.000000 | 2.829152 | 0.000000 | 5.093188 | 0 | 0.065122 | 4.635671 | 1.015640 | 0.461296 | ... | 4.446634 | 0.157178 | 0.616401 | 0.000000 | 4.039816 | 0.000000 | 4.714087 | 1.565475 | 0.860254 | 4.866979 |
5 rows × 630 columns
lps_response_corr = lps_response.corr()
“Elbow method” for determining number of clusters¶
The authors state that they used the “Elbow method” to determine the number of cluster centers. Essentially, you try a bunch of different \(k\), and see where there is a flattening out of the metric, like an elbow. There’s a few different variations on which metric to use, such as using the average distance to the cluster center, or the explained variance. Let’s try the distance to cluster center first, because scikit-learn makes it easy.
from sklearn.cluster import KMeans
##### cluster data into K=1..10 clusters #####
ks = np.arange(1, 11).astype(int)
X = lps_response_corr.values
kmeans = [KMeans(n_clusters=k).fit(X) for k in ks]
# Scikit-learn makes this easy by computing the distance to the nearest center
dist_to_center = [km.inertia_ for km in kmeans]
fig, ax = plt.subplots()
ax.plot(ks, dist_to_center, 'o-')
ax.set_ylabel('Sum of distance to nearest cluster center')
sns.despine()
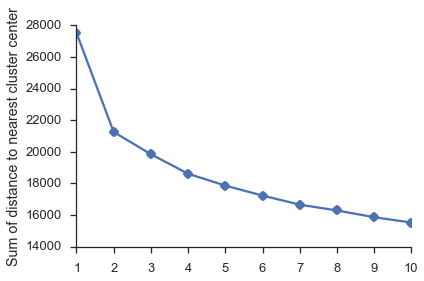
Not quite sure where the elbow is here. looks like there’s a big drop off after \(k=1\), but that could just be an illusion. Since they didn’t specify which version of the elbow method they used, I’m not going to investigate this further, and just see if we can see what they see with the \(k=5\) clusters that they found was optimal.
kmeans = KMeans(n_clusters=5)
lps_response_corr_clusters = kmeans.fit_predict(lps_response_corr.values)
lps_response_corr_clusters
array([3, 0, 4, 4, 1, 0, 3, 4, 2, 4, 1, 3, 2, 4, 3, 3, 1, 0, 1, 3, 1, 0, 2,
1, 1, 3, 3, 2, 4, 4, 1, 4, 4, 1, 4, 1, 3, 4, 2, 0, 2, 4, 2, 3, 0, 4,
1, 1, 4, 0, 0, 3, 4, 1, 1, 2, 1, 1, 1, 2, 0, 3, 4, 3, 3, 4, 2, 2, 4,
3, 1, 4, 1, 3, 4, 2, 2, 4, 2, 3, 3, 3, 0, 0, 4, 1, 2, 2, 2, 0, 0, 3,
0, 0, 4, 3, 3, 3, 3, 0, 0, 2, 1, 2, 1, 1, 2, 1, 2, 4, 2, 1, 1, 3, 4,
4, 1, 2, 4, 3, 4, 2, 2, 2, 0, 4, 4, 1, 0, 2, 3, 3, 4, 4, 1, 1, 4, 3,
2, 0, 1, 4, 2, 1, 4, 2, 4, 1, 0, 1, 1, 3, 3, 3, 3, 0, 0, 3, 1, 2, 2,
3, 4, 0, 0, 4, 2, 2, 2, 3, 3, 3, 3, 1, 3, 3, 0, 1, 2, 0, 0, 1, 2, 4,
1, 0, 3, 2, 0, 3, 1, 0, 0, 2, 4, 3, 0, 1, 1, 1, 3, 3, 2, 0, 3, 0, 4,
4, 4, 3, 2, 3, 3, 0, 4, 3, 4, 3, 1, 0, 3, 3, 3, 3, 3, 0, 4, 0, 1, 3,
3, 2, 4, 3, 4, 1, 1, 3, 0, 0, 2, 4, 2, 4, 4, 3, 0, 3, 0, 1, 4, 0, 0,
1, 1, 4, 1, 1, 1, 0, 4, 3, 4, 3, 3, 3, 3, 1, 3, 4, 4, 2, 2, 0, 2, 2,
1, 1, 1, 4, 1, 2, 4, 1, 2, 2, 1, 4, 1, 3, 0, 3, 2, 3, 1, 3, 3, 3, 2,
0, 2, 2, 2, 2, 4, 2, 3, 2, 4, 3, 2, 2, 3, 0, 4, 1, 1, 1, 1, 1, 0, 4,
0, 4, 4, 3, 0, 1, 1, 0, 0, 2, 0, 2, 1, 4, 3, 4, 1, 0, 3, 3, 1, 3, 2,
2, 3, 1, 1, 2, 4, 4, 1, 0, 0, 3, 4, 2, 1, 3, 3, 1, 0, 1, 1, 3, 3, 2,
3, 0, 1, 2, 3, 3, 0, 0, 0, 3, 4, 2, 2, 2, 2, 3, 3, 2, 1, 0, 0, 0, 0,
1, 3, 4, 4, 1, 4, 3, 3, 0, 1, 1, 1, 3, 1, 3, 3, 1, 0, 4, 4, 4, 3, 3,
3, 0, 3, 0, 2, 4, 0, 4, 1, 0, 1, 0, 0, 1, 0, 0, 2, 4, 0, 1, 3, 1, 3,
3, 0, 0, 0, 4, 3, 0, 0, 2, 3, 4, 4, 2, 3, 1, 0, 4, 3, 2, 3, 3, 0, 0,
2, 3, 0, 2, 0, 1, 1, 4, 3, 3, 0, 3, 4, 1, 0, 1, 4, 1, 4, 0, 4, 1, 0,
3, 1, 3, 1, 4, 3, 2, 2, 3, 3, 0, 1, 4, 4, 0, 0, 4, 1, 2, 2, 3, 2, 4,
0, 1, 3, 4, 2, 0, 0, 3, 3, 1, 1, 1, 3, 3, 0, 1, 3, 2, 3, 3, 1, 2, 1,
0, 3, 1, 3, 4, 4, 0, 2, 4, 2, 3, 4, 3, 4, 3, 4, 2, 4, 0, 0, 4, 3, 2,
2, 4, 1, 0, 2, 1, 3, 1, 3, 1, 2, 0, 0, 3, 1, 2, 0, 3, 3, 1, 2, 1, 1,
4, 2, 1, 3, 4, 3, 2, 1, 0, 4, 0, 3, 1, 4, 2, 2, 1, 3, 4, 3, 0, 4, 3,
4, 2, 2, 3, 2, 1, 1, 4, 2, 0, 0, 0, 3, 3, 3, 2, 2, 1, 0, 2, 3, 1, 4,
4, 3, 2, 2, 2, 0, 2, 0, 2], dtype=int32)
Now let’s create a dataframe with these genes in their cluster orders.
gene_to_cluster = dict(zip(lps_response_corr.columns, lps_response_corr_clusters))
dfs = []
for name, df in lps_response_corr.groupby(gene_to_cluster):
dfs.append(df)
lps_response_corr_ordered_by_clusters = pd.concat(dfs)
# Make symmetric, since we created this dataframe by smashing rows on top of each other, we need to reorder the columns
lps_response_corr_ordered_by_clusters = lps_response_corr_ordered_by_clusters.ix[:, lps_response_corr_ordered_by_clusters.index]
lps_response_corr_ordered_by_clusters.head()
| GENE | 1110038F14RIK | 2210009G21RIK | A430084P05RIK | AA960436 | AK141659 | AK163103 | ALCAM | ALPK2 | ARMC8 | BC147527 | ... | TNFAIP2 | TNFSF4 | TOR1AIP1 | TRA2A | TRIM26 | TRIM34 | TTC39C | USP12 | ZC3H12C | ZC3HAV1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GENE | |||||||||||||||||||||
| 1110038F14RIK | 1.000000 | 0.175230 | 0.043846 | 0.240304 | 0.150073 | -0.007459 | -0.075510 | 0.001210 | 0.078638 | -0.073983 | ... | -0.053588 | -0.085191 | 0.322774 | 0.096905 | -0.370932 | 0.451829 | 0.387727 | -0.257008 | 0.274102 | -0.163423 |
| 2210009G21RIK | 0.175230 | 1.000000 | 0.301786 | 0.454579 | -0.106546 | -0.122179 | 0.177472 | 0.215454 | 0.540303 | 0.078574 | ... | 0.230309 | -0.158622 | 0.019694 | 0.142045 | 0.053967 | 0.483106 | -0.085604 | 0.279262 | 0.153934 | 0.160710 |
| A430084P05RIK | 0.043846 | 0.301786 | 1.000000 | 0.001150 | 0.060210 | -0.173020 | 0.150884 | 0.429134 | 0.131837 | -0.069652 | ... | -0.341757 | -0.296639 | -0.192074 | -0.360383 | 0.025340 | 0.033636 | -0.227960 | -0.166541 | 0.200579 | 0.064736 |
| AA960436 | 0.240304 | 0.454579 | 0.001150 | 1.000000 | -0.361780 | 0.206889 | 0.174208 | 0.075687 | 0.394432 | 0.163830 | ... | 0.175022 | -0.271395 | 0.272221 | -0.222182 | 0.181522 | -0.094028 | 0.218182 | 0.396040 | -0.159072 | 0.048122 |
| AK141659 | 0.150073 | -0.106546 | 0.060210 | -0.361780 | 1.000000 | -0.287830 | -0.370827 | 0.143026 | -0.019682 | -0.157671 | ... | -0.295535 | 0.194073 | -0.232992 | 0.061276 | -0.032583 | 0.411637 | -0.182131 | 0.018036 | 0.175434 | -0.288042 |
5 rows × 630 columns
The next step is to get the principal-component reduced data, using only the LPS response genes. We can do this in flotilla using study.expression.reduce.
reduced = study.expression.reduce(singles_ids, feature_ids=lps_response_genes)
We can get the principal components using reduced.components_ (similar interface as scikit-learn).
reduced.components_.head()
| MOV10 | PPAP2B | LASS6 | TMCO3 | CPD | AK138792 | TARM1 | P4HA1 | CD180 | SMG7 | ... | OAS1B | OAS1G | AK151815 | GTPBP2 | PRPF38A | SLC7A11 | PCDH7 | GNA13 | PTPRJ | ATF3 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| pc_1 | 0.035299 | 0.038725 | -0.006343 | 0.014219 | 0.033734 | -0.079831 | 0.032886 | 0.034783 | 0.033719 | -0.048453 | ... | -0.022490 | 0.031091 | -0.021397 | 0.034917 | 0.001745 | 0.058000 | 0.007748 | 0.000767 | 0.016012 | 0.018020 |
| pc_2 | 0.055310 | 0.002925 | -0.043986 | -0.024020 | -0.061957 | -0.016327 | 0.002882 | -0.003178 | 0.050055 | 0.038601 | ... | 0.012240 | 0.052127 | 0.009120 | 0.077015 | 0.072064 | -0.080902 | -0.056607 | 0.068444 | -0.072533 | 0.068088 |
| pc_3 | 0.000374 | 0.099514 | -0.039636 | 0.003997 | -0.000575 | -0.042212 | -0.056827 | 0.015571 | -0.039811 | 0.005398 | ... | -0.010524 | -0.009277 | -0.102462 | -0.043913 | -0.052513 | -0.030622 | 0.022607 | -0.002503 | 0.023997 | -0.054205 |
| pc_4 | 0.022491 | 0.002342 | 0.009422 | -0.034725 | 0.025866 | -0.009656 | -0.027689 | -0.089803 | -0.046888 | 0.002274 | ... | -0.003404 | -0.070307 | -0.007025 | 0.003407 | -0.048078 | 0.028099 | 0.032970 | -0.066284 | 0.010371 | -0.006108 |
| pc_5 | -0.025743 | -0.009200 | -0.030187 | -0.061283 | 0.010464 | 0.032668 | 0.012223 | -0.047623 | -0.047351 | 0.045909 | ... | -0.074817 | 0.044218 | -0.000884 | -0.000597 | -0.033893 | -0.018108 | -0.012669 | -0.025833 | -0.044248 | -0.001995 |
5 rows × 630 columns
pc_components = reduced.components_.ix[:2, lps_response_corr_ordered_by_clusters.index].T
pc_components.head()
| pc_1 | pc_2 | |
|---|---|---|
| GENE | ||
| 1110038F14RIK | -0.007729 | -0.005858 |
| 2210009G21RIK | -0.006981 | 0.002916 |
| A430084P05RIK | 0.014550 | 0.022191 |
| AA960436 | 0.002159 | 0.014470 |
| AK141659 | 0.016902 | -0.009151 |
import matplotlib as mpl
fig = plt.figure(figsize=(12, 10))
gs = gridspec.GridSpec(2, 2, wspace=0.1, hspace=0.1, width_ratios=[1, .2], height_ratios=[1, .1])
corr_ax = fig.add_subplot(gs[0, 0])
corr_cbar_ax = fig.add_subplot(gs[1, 0])
pc_ax = fig.add_subplot(gs[0, 1:])
pc_cbar_ax = fig.add_subplot(gs[1:, 1:])
sns.heatmap(lps_response_corr_ordered_by_clusters, linewidth=0, ax=corr_ax, cbar_ax=corr_cbar_ax,
cbar_kws=dict(orientation='horizontal'))
sns.heatmap(pc_components, cmap=mpl.cm.PRGn, linewidth=0, ax=pc_ax, cbar_ax=pc_cbar_ax,
cbar_kws=dict(orientation='horizontal'))
corr_ax.set_xlabel('')
corr_ax.set_ylabel('')
corr_ax.set_xticks([])
corr_ax.set_yticks([])
pc_ax.set_yticks([])
pc_ax.set_ylabel('')
<matplotlib.text.Text at 0x10f37d5d0>
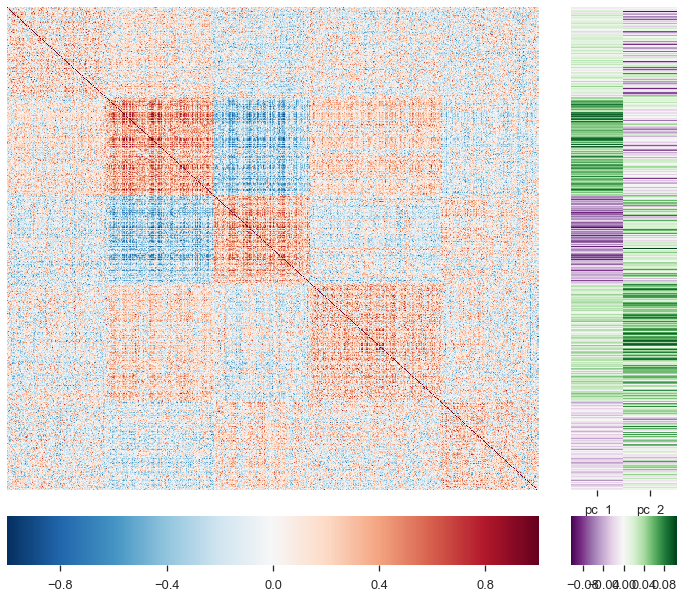
This looks pretty similar, maybe just rearranged cluster order. Let’s check what their data looks like when you plot this.
Their PC scores and clusters for the genes¶
gene_pc_clusters = pd.read_excel('nature12172-s1/Supplementary_Table5.xls', index_col=0)
gene_pc_clusters.head()
| Annotation | Cluster | PC1 Score | PC2 Score | |
|---|---|---|---|---|
| Gene | ||||
| LNPEP | NaN | 1 | 0.232368 | 0.677266 |
| TOR1AIP2 | Antiv | 1 | -0.075934 | 1.485877 |
| TNFSF4 | NaN | 1 | 0.497893 | -0.562412 |
| CFB | Inflam | 1 | -0.394318 | 1.277749 |
| H2-T10 | NaN | 1 | 0.514947 | -0.698538 |
data = lps_response_corr.ix[gene_pc_clusters.index, gene_pc_clusters.index].dropna(how='all', axis=0).dropna(how='all', axis=1)
fig = plt.figure(figsize=(12, 10))
gs = gridspec.GridSpec(2, 2, wspace=0.1, hspace=0.1, width_ratios=[1, .2], height_ratios=[1, .1])
corr_ax = fig.add_subplot(gs[0, 0])
corr_cbar_ax = fig.add_subplot(gs[1, 0])
pc_ax = fig.add_subplot(gs[0, 1:])
pc_cbar_ax = fig.add_subplot(gs[1:, 1:])
sns.heatmap(data, linewidth=0, square=True, vmin=-1, vmax=1, ax=corr_ax, cbar_ax=corr_cbar_ax, cbar_kws=dict(orientation='horizontal'))
sns.heatmap(gene_pc_clusters.ix[:, ['PC1 Score', 'PC2 Score']], linewidth=0, cmap=mpl.cm.PRGn,
ax=pc_ax, cbar_ax=pc_cbar_ax, cbar_kws=dict(orientation='horizontal'), xticklabels=False, yticklabels=False)
corr_ax.set_xlabel('')
corr_ax.set_ylabel('')
corr_ax.set_xticks([])
corr_ax.set_yticks([])
pc_ax.set_yticks([])
pc_ax.set_ylabel('');
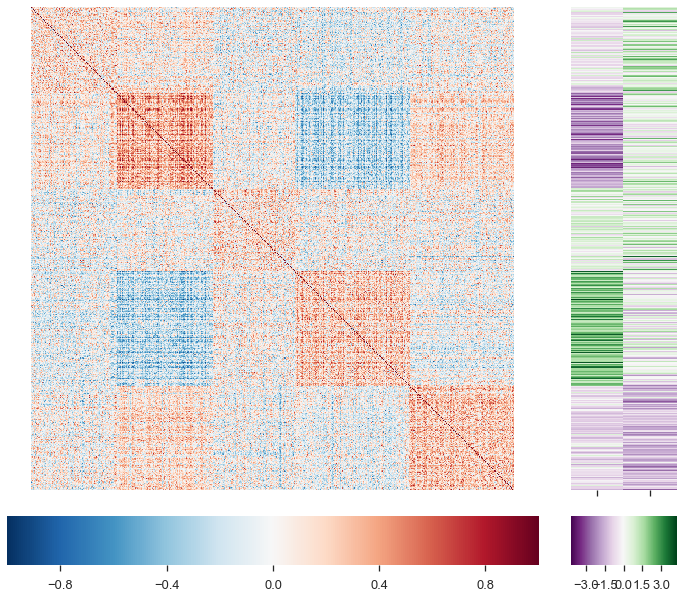
Sure enough, if I use their annotations, I get exactly that. Though there were two genes in their file that I didn’t have in the lps_response_corr data:
gene_pc_clusters.index.difference(lps_response_corr.index)
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-53-f11acbabb21a> in <module>()
----> 1 gene_pc_clusters.index.difference(lps_response_corr.index)
/usr/local/lib/python2.7/site-packages/pandas/core/index.pyc in difference(self, other)
1325 result_name = self.name if self.name == other.name else None
1326
-> 1327 theDiff = sorted(set(self) - set(other))
1328 return Index(theDiff, name=result_name)
1329
TypeError: can't compare datetime.datetime to unicode
Oh joy, another datetime error, just like we had with expression2... Looking back at the original Excel file, there is one gene that Excel mangled to be a date:
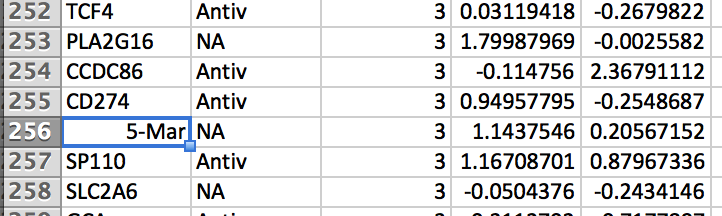
Please, can we start using just plain ole ``.csv``s for supplementary data! Excel does NOT preserve strings if they start with numbers, and instead thinks they are dates.
import collections
collections.Counter(gene_pc_clusters.index.map(type))
Counter({<type 'unicode'>: 631, <type 'datetime.datetime'>: 1})
Yep, it’s just that one that got mangled.... oh well.
gene_pc_clusters_genes = set(filter(lambda x: isinstance(x, unicode), gene_pc_clusters.index))
gene_pc_clusters_genes.difference(lps_response_corr.index)
{u'RPS6KA2'}
So, “RPS6KA2” is the only gene that was in their list of genes and not in mine.
Supplementary figures¶
Now we get to have even more fun by plotting the Supplementary figures! :D
Ironically, the supplementary figures are usually way easier to access (like not behind a paywall), and yet they’re usually the documents that really have the crucial information about the experiments.
Supplementary Figure 1¶
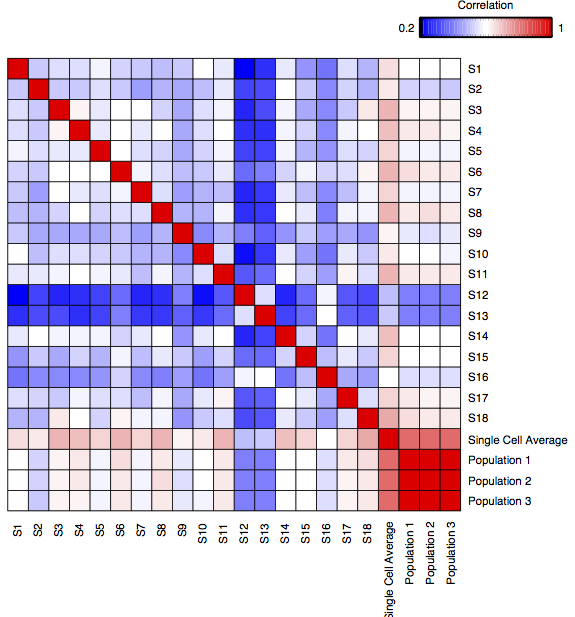
Supplementary figure 1, a correlation plot
singles_mean = study.expression.singles.mean()
singles_mean.name = 'Single cell average'
# Need to convert "average_singles" to a DataFrame instead of a single-row Series
singles_mean = pd.DataFrame(singles_mean)
singles_mean.head()
| Single cell average | |
|---|---|
| GENE | |
| NPL | 1.075740 |
| QK | 2.019888 |
| AK163153 | 1.429369 |
| PARK2 | 0.596479 |
| AGPAT4 | 2.021294 |
data_for_correlations = pd.concat([study.expression.singles, singles_mean.T, study.expression.pooled])
# Take the transpose of the data, because the plotting algorithm calculates correlations between columns,
# And we want the correlations between samples, not features
data_for_correlations = data_for_correlations.T
data_for_correlations.head()
# %time sns.corrplot(data_for_correlations)
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | ... | S13 | S14 | S15 | S16 | S17 | S18 | Single cell average | P1 | P2 | P3 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GENE | |||||||||||||||||||||
| NPL | 4.290577 | 0.000000 | 4.860293 | 0.090829 | 0.000000 | 0.000000 | 4.730129 | 4.657090 | 0.112641 | 0.000000 | ... | 0.110470 | 0.099121 | 0.100920 | 0.206361 | 0.104884 | 0.000000 | 1.075740 | 2.093019 | 2.044724 | 2.742480 |
| QK | 5.038477 | 4.183371 | 3.847854 | 0.066797 | 3.305915 | 0.114225 | 3.730270 | 2.750103 | 0.134389 | 0.760353 | ... | 3.395885 | 2.294456 | 0.301120 | 3.547688 | 2.185832 | 0.040923 | 2.019888 | 3.869102 | 3.690982 | 3.671838 |
| AK163153 | 1.249363 | 1.947622 | 1.082463 | 1.119633 | 1.267464 | 0.901824 | 1.033401 | 0.978591 | 1.220720 | 1.035237 | ... | 2.103135 | 1.110511 | 1.202271 | 4.446612 | 1.367261 | 0.428320 | 1.429369 | 0.605094 | 0.392494 | 0.284990 |
| PARK2 | 0.540694 | 0.500426 | 0.604097 | 0.418703 | 0.000000 | 0.601280 | 0.404931 | 0.552874 | 0.343271 | 0.844120 | ... | 0.755072 | 1.109400 | 0.807534 | 0.586962 | 0.485122 | 0.091469 | 0.596479 | 0.815242 | 0.267032 | 0.645365 |
| AGPAT4 | 0.095072 | 5.868557 | 4.137252 | 0.066015 | 0.000000 | 4.750107 | 0.069345 | 4.130618 | 3.328758 | 0.000000 | ... | 0.000000 | 4.430612 | 0.000000 | 0.000000 | 4.219120 | 0.171028 | 2.021294 | 2.854144 | 2.139655 | 2.806291 |
5 rows × 22 columns
fig, ax = plt.subplots(figsize=(10, 10))
sns.corrplot(data_for_correlations, ax=ax)
sns.despine()
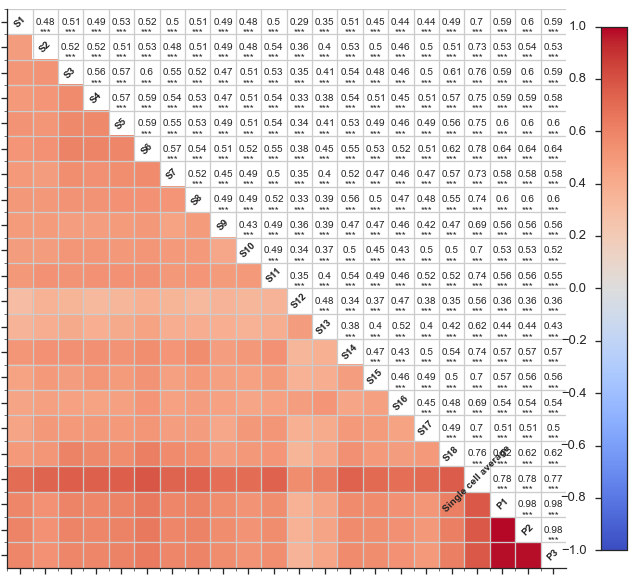
Notice that this is mostly red, while in the figure from the paper, it was both blue and red. This is because the colormap started at 0.2 (not negative), and was centered with white at about 0.6. I see that they’re trying to emphasize how much more correlated the pooled samples are to each other, but I think a simple sequential map would have been more effective.
Supplementary Figures 2 and 3¶
Supplementary Figure 2 and Figure 3 are from FISH and raw sequence data, and are out of the scope of this computational reproduction.
Supplementary Figure 4¶
Supplementary Figure 4 was from published data, however the citation in the Supplementary Information (#23) was a machine-learning book, and #23 in the main text citations was a review of probabilistic graphical models, neither of which have the mouse embryonic stem cells or mouse embryonic fibroblasts used in the figure.
Supplementary Figure 5¶
For this figure, we can only plot 5d, since it’s derived directly from a table in their dataset.
Warning: these data are going to require some serious cleaning. Yay data janitorial duties!
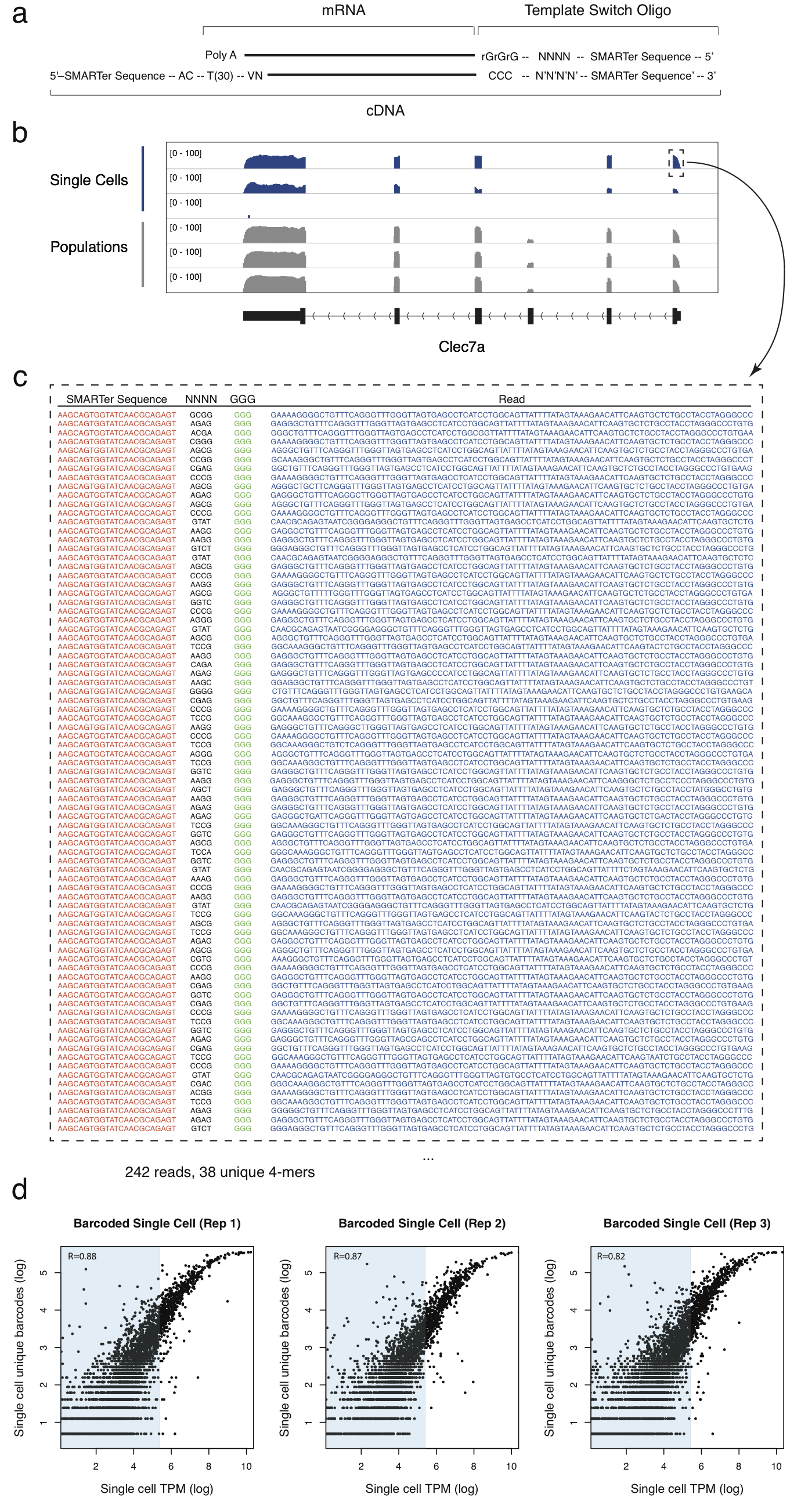
Supplementary Figure 5d¶
barcoded = pd.read_excel('nature12172-s1/Supplementary_Table7.xlsx')
barcoded.head()
| TPM | Unnamed: 1 | Unnamed: 2 | Unnamed: 3 | Unique Barcodes | Unnamed: 5 | Unnamed: 6 | |
|---|---|---|---|---|---|---|---|
| GENE | MB_S1 | MB_S2 | MB_S3 | NaN | MB_S1 | MB_S2 | MB_S3 |
| 0610007L01RIK | 0 | 0 | 5.595054 | NaN | 0 | 0 | 0 |
| 0610007P14RIK | 76.25091 | 38.77614 | 0.1823286 | NaN | 23 | 8 | 0 |
| 0610007P22RIK | 24.26729 | 50.24694 | 17.74422 | NaN | 14 | 5 | 6 |
| 0610008F07RIK | 0 | 0 | 0 | NaN | 0 | 0 | 0 |
The first three columns are TPM calculated from the three samples that have molecular barcodes, and the last three columns are the integer counts of molecular barcodes from the three molecular barcode samples.
Let’s remove the “Unnamed: 3” column which is all NaNs. We’ll do that with the .dropna method, specifying axis=1 for columns and how="all" to make sure only columns that have ALL NaNs are removed.
barcoded = barcoded.dropna(how='all', axis=1)
barcoded.head()
| TPM | Unnamed: 1 | Unnamed: 2 | Unique Barcodes | Unnamed: 5 | Unnamed: 6 | |
|---|---|---|---|---|---|---|
| GENE | MB_S1 | MB_S2 | MB_S3 | MB_S1 | MB_S2 | MB_S3 |
| 0610007L01RIK | 0 | 0 | 5.595054 | 0 | 0 | 0 |
| 0610007P14RIK | 76.25091 | 38.77614 | 0.1823286 | 23 | 8 | 0 |
| 0610007P22RIK | 24.26729 | 50.24694 | 17.74422 | 14 | 5 | 6 |
| 0610008F07RIK | 0 | 0 | 0 | 0 | 0 | 0 |
Next, let’s drop that pesky “GENE” row. Don’t worry, we’ll get the sample ID names back next.
barcoded = barcoded.drop('GENE', axis=0)
barcoded.head()
| TPM | Unnamed: 1 | Unnamed: 2 | Unique Barcodes | Unnamed: 5 | Unnamed: 6 | |
|---|---|---|---|---|---|---|
| 0610007L01RIK | 0 | 0 | 5.595054 | 0 | 0 | 0 |
| 0610007P14RIK | 76.25091 | 38.77614 | 0.1823286 | 23 | 8 | 0 |
| 0610007P22RIK | 24.26729 | 50.24694 | 17.74422 | 14 | 5 | 6 |
| 0610008F07RIK | 0 | 0 | 0 | 0 | 0 | 0 |
| 0610009B22RIK | 67.12981 | 115.1393 | 55.98812 | 11 | 18 | 8 |
We’ll create a pandas.MultiIndex from the tuples of (sample_id, measurement_type) pair.
columns = pd.MultiIndex.from_tuples([('MB_S1', 'TPM'),
('MB_S2', 'TPM'),
('MB_S3', 'TPM'),
('MB_S1', 'Unique Barcodes'),
('MB_S2', 'Unique Barcodes'),
('MB_S3', 'Unique Barcodes')])
barcoded.columns = columns
barcoded = barcoded.sort_index(axis=1)
barcoded.head()
| MB_S1 | MB_S2 | MB_S3 | ||||
|---|---|---|---|---|---|---|
| TPM | Unique Barcodes | TPM | Unique Barcodes | TPM | Unique Barcodes | |
| 0610007L01RIK | 0 | 0 | 0 | 0 | 5.595054 | 0 |
| 0610007P14RIK | 76.25091 | 23 | 38.77614 | 8 | 0.1823286 | 0 |
| 0610007P22RIK | 24.26729 | 14 | 50.24694 | 5 | 17.74422 | 6 |
| 0610008F07RIK | 0 | 0 | 0 | 0 | 0 | 0 |
| 0610009B22RIK | 67.12981 | 11 | 115.1393 | 18 | 55.98812 | 8 |
For the next move, we’re going to do some crazy pandas-fu. First we’re going to transpose, then reset_index of the transpose. Just so you know what this looks like, it’s this.
barcoded.T.reset_index().head()
| level_0 | level_1 | 0610007L01RIK | 0610007P14RIK | 0610007P22RIK | 0610008F07RIK | 0610009B22RIK | 0610009D07RIK | 0610009O20RIK | 0610010B08RIK | ... | ZWILCH | ZWINT | ZXDA | ZXDB | ZXDC | ZYG11A | ZYG11B | ZYX | ZZEF1 | ZZZ3 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | MB_S1 | TPM | 0 | 76.25091 | 24.26729 | 0 | 67.12981 | 132.2392 | 17.03907 | 0.01375923 | ... | 0 | 206.8494 | 0 | 0 | 0 | 0 | 0.01985733 | 55.28996 | 0.09482778 | 0 |
| 1 | MB_S1 | Unique Barcodes | 0 | 23 | 14 | 0 | 11 | 29 | 3 | 1 | ... | 0 | 33 | 0 | 0 | 0 | 0 | 0 | 6 | 0 | 0 |
| 2 | MB_S2 | TPM | 0 | 38.77614 | 50.24694 | 0 | 115.1393 | 49.16287 | 0 | 0 | ... | 0 | 48.7729 | 0 | 0 | 0 | 0 | 7.894789 | 135.1977 | 0 | 4.272594 |
| 3 | MB_S2 | Unique Barcodes | 0 | 8 | 5 | 0 | 18 | 11 | 0 | 0 | ... | 0 | 10 | 0 | 0 | 0 | 0 | 0 | 7 | 0 | 0 |
| 4 | MB_S3 | TPM | 5.595054 | 0.1823286 | 17.74422 | 0 | 55.98812 | 203.6302 | 0 | 0.4914763 | ... | 0 | 54.51386 | 1.120081 | 0 | 0 | 0 | 0.1238624 | 340.7358 | 0.6677646 | 0 |
5 rows × 27725 columns
Next, we’re going to transform the data into a tidy format, with separate columns for sample ids, measurement types, the gene that was measured, and its measurement value.
barcoded_tidy = pd.melt(barcoded.T.reset_index(), id_vars=['level_0', 'level_1'])
barcoded_tidy.head()
| level_0 | level_1 | variable | value | |
|---|---|---|---|---|
| 0 | MB_S1 | TPM | 0610007L01RIK | 0 |
| 1 | MB_S1 | Unique Barcodes | 0610007L01RIK | 0 |
| 2 | MB_S2 | TPM | 0610007L01RIK | 0 |
| 3 | MB_S2 | Unique Barcodes | 0610007L01RIK | 0 |
| 4 | MB_S3 | TPM | 0610007L01RIK | 5.595054 |
Now let’s rename these columns into something more useful, instead of “level_0”
barcoded_tidy = barcoded_tidy.rename(columns={'level_0': 'sample_id', 'level_1': 'measurement', 'variable': 'gene_name'})
barcoded_tidy.head()
| sample_id | measurement | gene_name | value | |
|---|---|---|---|---|
| 0 | MB_S1 | TPM | 0610007L01RIK | 0 |
| 1 | MB_S1 | Unique Barcodes | 0610007L01RIK | 0 |
| 2 | MB_S2 | TPM | 0610007L01RIK | 0 |
| 3 | MB_S2 | Unique Barcodes | 0610007L01RIK | 0 |
| 4 | MB_S3 | TPM | 0610007L01RIK | 5.595054 |
Next, we’re going to take some seemingly-duplicating steps, but trust me, it’ll make the data easier.
barcoded_tidy['TPM'] = barcoded_tidy.value[barcoded_tidy.measurement == 'TPM']
barcoded_tidy['Unique Barcodes'] = barcoded_tidy.value[barcoded_tidy.measurement == 'Unique Barcodes']
Fill the values of the “TPM“‘s forwards, since they appear first, and fill the values of the “Unique Barcodes” backwards, since they’re second
barcoded_tidy.TPM = barcoded_tidy.TPM.ffill()
barcoded_tidy['Unique Barcodes'] = barcoded_tidy['Unique Barcodes'].bfill()
barcoded_tidy.head()
| sample_id | measurement | gene_name | value | TPM | Unique Barcodes | |
|---|---|---|---|---|---|---|
| 0 | MB_S1 | TPM | 0610007L01RIK | 0 | 0.000000 | 0 |
| 1 | MB_S1 | Unique Barcodes | 0610007L01RIK | 0 | 0.000000 | 0 |
| 2 | MB_S2 | TPM | 0610007L01RIK | 0 | 0.000000 | 0 |
| 3 | MB_S2 | Unique Barcodes | 0610007L01RIK | 0 | 0.000000 | 0 |
| 4 | MB_S3 | TPM | 0610007L01RIK | 5.595054 | 5.595054 | 0 |
Drop the “measurement” column and drop duplicate rows.
barcoded_tidy = barcoded_tidy.drop('measurement', axis=1)
barcoded_tidy = barcoded_tidy.drop_duplicates()
barcoded_tidy.head()
| sample_id | gene_name | value | TPM | Unique Barcodes | |
|---|---|---|---|---|---|
| 0 | MB_S1 | 0610007L01RIK | 0 | 0.000000 | 0 |
| 2 | MB_S2 | 0610007L01RIK | 0 | 0.000000 | 0 |
| 4 | MB_S3 | 0610007L01RIK | 5.595054 | 5.595054 | 0 |
| 5 | MB_S3 | 0610007L01RIK | 0 | 5.595054 | 0 |
| 6 | MB_S1 | 0610007P14RIK | 76.25091 | 76.250913 | 23 |
barcoded_tidy['log TPM'] = np.log(barcoded_tidy.TPM)
barcoded_tidy['log Unique Barcodes'] = np.log(barcoded_tidy['Unique Barcodes'])
Now we can use the convenient linear model plot (lmplot) in seaborn to plot these three samples together!
sns.lmplot('log TPM', 'log Unique Barcodes', barcoded_tidy, col='sample_id')
<seaborn.axisgrid.FacetGrid at 0x123293390>
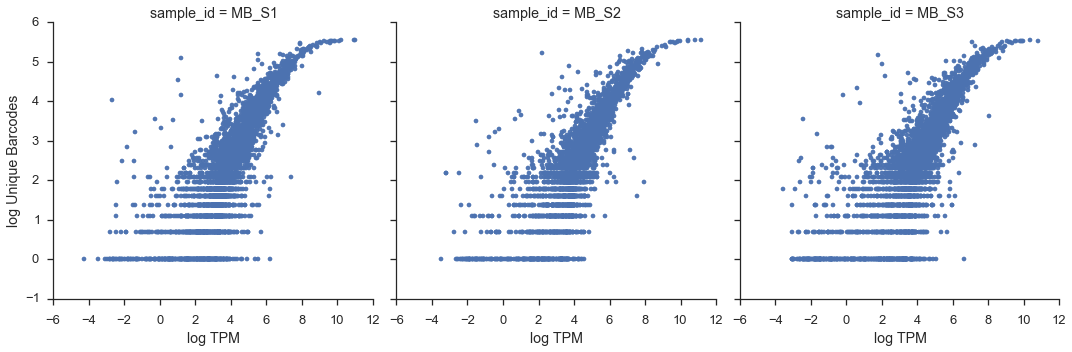
Conclusions¶
While there may be minor, undocumented, differences between the methods presented in the manuscript and the figures, the application of `flotilla <https://github.com/YeoLab/flotilla>`_ presents an opportunity to avoid these types of inconsistencies by strictly documenting every change to code and every transformation of the data. The biology the authors found is clearly real, as they did the knockout experiment of Ifnr-/- and saw that indeed the maturation process was affected, and Stat2 and Irf7 had much lower expression, as with the “maturing” cells in the data.